题目内容
函数y=f(x)是偶函数,当x>0时,f(x)=x+| 4 | x |
分析:利用偶函数的定义求出函数在[-3,-1]上的解析式,利用导数求出函数的最值,求出差.
解答:解:当x∈[-3,-1]时-x∈[1,3]
∵当x>0时,f(x)=x+
∴f(-x)=-x-
∵函数y=f(x)是偶函数
∴f(x)=-x-
,x∈[-3,-1]
∵f′(x)=-1+
=
当-3≤x<-2时,f′(x)<0;当-2<x<-1时,f′(x)>0
所以当x=-2时,函数有最小值4;当x=-3时f(-3)=
;
当x=-1时,f(-1)=5所以函数的最大值为5
所以m=5,n=4,
故m-n=1,
故答案为1.
∵当x>0时,f(x)=x+
| 4 |
| x |
∴f(-x)=-x-
| 4 |
| x |
∵函数y=f(x)是偶函数
∴f(x)=-x-
| 4 |
| x |
∵f′(x)=-1+
| 4 |
| x2 |
| 4-x2 |
| x2 |
当-3≤x<-2时,f′(x)<0;当-2<x<-1时,f′(x)>0
所以当x=-2时,函数有最小值4;当x=-3时f(-3)=
| 13 |
| 3 |
当x=-1时,f(-1)=5所以函数的最大值为5
所以m=5,n=4,
故m-n=1,
故答案为1.
点评:本题考查偶函数的定义、利用导数求函数的单调性及求函数的最值.

练习册系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: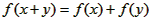 ,
,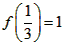 ,且当x>0时,f(x)>0。
,且当x>0时,f(x)>0。  ,求x的取值范围。
,求x的取值范围。