题目内容
甲有一个放有5个红球，4个白球，1个黄球的箱子；乙也有一个放有5个红球，4个白球，1个黄球的箱子，两人各自从自己的箱子里任取一球比颜色，规定同色时甲胜，异色时为乙胜，请问这个游戏公平吗?请说明理由；如果不公平，请你为吃亏方在箱子中球的总个数不变的原则下，调整红、白、黄球的个数，使这个游戏规则公平．
解：由题意，两人各自从自己的箱子里任取一球的颜色共有
=100(种)不同情形，每种情形是等可能的，记甲获胜为事件A.
则P(A)=
所以甲获胜的概率小于乙获胜的概率，这个游戏规则是不公平的；
设将甲箱子中的球调整为红球x个，白球y个，黄球z个，且
x+y+z=10，x、y、z∈N，能使游戏规则公平．
则P(A)=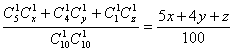
=
∴4x+3y=40，x∈N，y∈N，0≤x≤10，0≤y≤10
符合条件的整数解只有x=10，y=0,z=0
∴甲的箱子中全为红球时，这个游戏规则是公平的．
练习册系列答案
相关题目
的分布列及数学期望；
).
；
；
；②P（B|A1）=
；③A1，A2，A3是两两互斥的事件；④事件B与A1事件相互独立； ⑤P（B）的值不能确定，因为它与A1，A2，A3中哪一个发生有关。