题目内容
若A是圆x2+y2=16上的一个动点,过点A向y轴作垂线,垂足为B,则线段AB中点C的轨迹方程为( )
分析:设出C点坐标为(x,y),由已知中过点A向y轴作垂线,垂足为B,C为线段AB中点,我们易得A点坐标,由A在圆x2+y2=16上,满足圆的方程,易得到x,y之间的关系式,即线段AB中点C的轨迹方程.
解答:解:设C点坐标为(x,y),则A点坐标为(2x,y)
由于A点是圆x2+y2=16上的一个动点
故(2x)2+y2=16
即4x2+y2=16
故选D
由于A点是圆x2+y2=16上的一个动点
故(2x)2+y2=16
即4x2+y2=16
故选D
点评:本题考查的知识点是轨迹方程,坐标法是求曲线轨迹方程最常用的方法,其步骤为:设出动点坐标,根据已知条件构造方程,化简方程得到结果.

练习册系列答案
相关题目
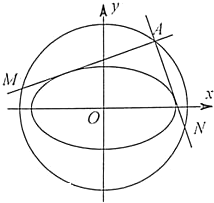 (2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆
(2013•绍兴一模)已知A是圆x2+y2=4上的一个动点,过点A作两条直线l1,l2,它们与椭圆