题目内容
在圆 上任取一点
上任取一点 ,设点
,设点 在
在 轴上的正投影为点
轴上的正投影为点 .当点
.当点 在圆上运动时,动点
在圆上运动时,动点 满足
满足 ,动点
,动点 形成的轨迹为曲线
形成的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)已知点 ,若
,若 、
、 是曲线
是曲线 上的两个动点,且满足
上的两个动点,且满足 ,求
,求 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2)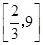 .
.
【解析】
试题分析:(1)解法一是从条件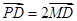 得到点
得到点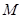 为线段
为线段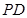 的中点,设点
的中点,设点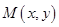 ,从而得到点
,从而得到点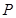 的坐标为
的坐标为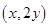 ,利用点
,利用点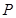 在圆
在圆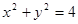 上,其坐标满足圆的方程,代入化简得到曲线
上,其坐标满足圆的方程,代入化简得到曲线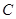 的方程;解法二是利用相关点法,设点
的方程;解法二是利用相关点法,设点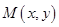 ,点
,点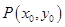 ,通过条件
,通过条件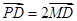 确定点
确定点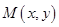 与点
与点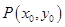 的坐标之间的关系,并利用点
的坐标之间的关系,并利用点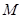 的坐标表示点
的坐标表示点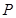 的坐标,再借助点
的坐标,再借助点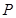 在圆
在圆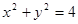 上,其坐标满足圆的方程,代入化简得到曲线
上,其坐标满足圆的方程,代入化简得到曲线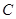 的方程;(2)先利用条件
的方程;(2)先利用条件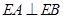 将
将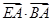 化简为
化简为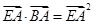 ,并设点
,并设点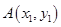 ,从而得到
,从而得到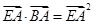 的坐标表达式,结合点
的坐标表达式,结合点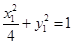 ,将
,将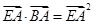 的代数式化为以
的代数式化为以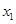 的二次函数,结合
的二次函数,结合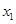 的取值范围,求出
的取值范围,求出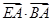 的取值范围.
的取值范围.
试题解析:(1)解法1:由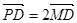 知点
知点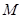 为线段
为线段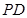 的中点.
的中点.
设点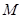 的坐标是
的坐标是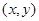 ,则点
,则点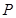 的坐标是
的坐标是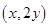 .
.
因为点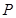 在圆
在圆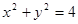 上,所以
上,所以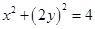 .
.
所以曲线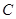 的方程为
的方程为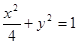 ;
;
解法2:设点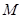 的坐标是
的坐标是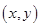 ,点
,点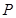 的坐标是
的坐标是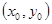 ,
,
由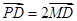 得,
得,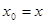 ,
,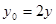 .
.
因为点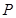
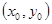 在圆
在圆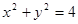 上,
所以
上,
所以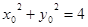 . ①
. ①
把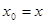 ,
,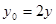 代入方程①,得
代入方程①,得 .
.
所以曲线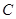 的方程为
的方程为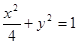 ;
;
(2)解:因为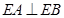 ,所以
,所以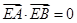 .
.
所以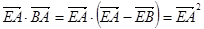 .
.
设点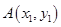 ,则
,则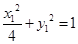 ,即
,即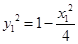 .
.
所以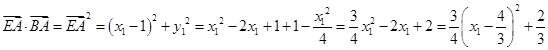 ,
,
因为点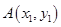 在曲线
在曲线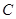 上,所以
上,所以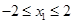 .
.
所以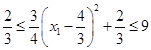 .
.
所以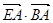 的取值范围为
的取值范围为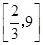 .
.
考点:1.相关点法求轨迹方程;2.平面向量的数量积;3.二次函数的最值

练习册系列答案
相关题目
 = 2
= 2 .
. 的方程;
的方程; ,点
,点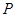 为曲线
为曲线 到点
到点 ;
; 的条件下,设△
的条件下,设△ 的面积为
的面积为 (
( 是坐标原点,
是坐标原点, 的点),以
的点),以 .若正数
.若正数 满足
满足 ,问
,问 = 2
= 2 .
. 的方程;
的方程; ,点
,点 为曲线
为曲线 到点
到点 ;
; 的条件下,设△
的条件下,设△ 的面积为
的面积为 (
( 是坐标原点,
是坐标原点, 的点),以
的点),以 .若正数
.若正数 满足
满足 ,问
,问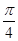 ;
; 。
。