题目内容
设
是两个互相垂直的单位向量，
，
，若
⊥
，则λ的值为 ．
【答案】分析：利用向量垂直的充要条件：向量垂直数量积等于0，列出方程求出λ．
解答：解：∵
∴
∵
∴
即
=0
2-λ=0
解得λ=2
故答案为2
点评：本题考查两向量垂直的充要条件：数量积等于0；单位向量的定义．
解答：解：∵
∴∵
∴即
=02-λ=0
解得λ=2
故答案为2
点评：本题考查两向量垂直的充要条件：数量积等于0；单位向量的定义．
练习册系列答案
阅读快车系列答案
相关题目
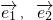是两个互相垂直的单位向量，
，
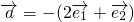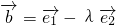，若
⊥
，则λ的值为 ________．
是两个互相垂直的单位向量，已知向量
且向量
，
．
是两个互相垂直的单位向量，
的值为 .