Question

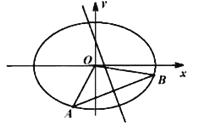
【题目】已知椭圆：（），过原点的两条直线和分别与交于点、和、，得到平行四边形.

（1）当为正方形时，求该正方形的面积.

（2）若直线和关于轴对称，上任意一点到和的距离分别为和，当为定值时，求此时直线和的斜率及该定值.

（3）当为菱形，且圆内切于菱形时，求，满足的关系式.

Answer 1

【答案】（1）；（2）和，；（3）.

【解析】

(1)直线和的方程为和利用，可得，根据对称性，可得正方形的面积；

(2) 利用距离公式，结合为定值，即可证明结论；(3)设出切线的方程与椭圆方程联立，分类讨论，即可求满足的关系式.

（1）因为为正方形，所以直线和的方程为和.

点、的坐标、为方程组的实数解，

将代入椭圆方程，解得.

根据对称性，可得正方形的面积.

（2）由题设，不妨设直线的方程为（），于是直线的方程为.

设，于是有，又，，

，将代入上式，

得，

对于任意，上式为定值，必有，即，

因此，直线和的斜率分别为和，

此时.

（3）设与圆相切的切点坐标为，于是切线的方程为.

点、的坐标、为方程组的实数解.

① 当或时，均为正方形，椭圆均过点，于是有.

② 当且时，将代入，

整理得，

于是，

同理可得.

因为为菱形，所以，

得，即，

于是，

整理得，由，

得，即.

综上，，满足的关系式为.