题目内容
设A，B为非空集合，定义A△B={x|x∈A∪B且x∉A∩B}，已知A={x|1＜x＜3}，B={x|2≤x≤4}，则A△B=（ ）
分析：根据已知中的集合A，B，先计算出A∪B和A∩B，进而根据A△B={x|x∈A∪B且x∉A∩B}，得到答案．
解答：解：∵A={x|1＜x＜3}，B={x|2≤x≤4}，
∴A∪B={x|1＜x≤4}，
A∩B={x|2≤x＜3}，
∴A△B={x|x∈A∪B且x∉A∩B}={x|1＜x＜2，或3≤x≤4}=（1，2）∪[3，4]，
故选：B
∴A∪B={x|1＜x≤4}，
A∩B={x|2≤x＜3}，
∴A△B={x|x∈A∪B且x∉A∩B}={x|1＜x＜2，或3≤x≤4}=（1，2）∪[3，4]，
故选：B
点评：本题考查的知识点是集合的交集和并集运算，正确理解新定义A△B={x|x∈A∪B且x∉A∩B}，是解答的关键．
练习册系列答案
相关题目
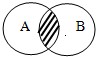1、设A、B为非空集合，定义集合A*B为如图非阴影部分表示的集合，若A={x|y=| 2x-x2 |
| A、（0，2） |
| B、[0，1]∪[2，+∞） |
| C、（1，2] |
| D、[0，1]∪（2，+∞） |
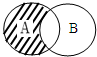设A、B为非空集合，定义运算A*B为如图阴影部分表示的集合，若