题目内容
设A、B为非空集合，定义集合A+B={x|x∈A或x∈B且x∉A∩B}，若P={x|y=| x2-3x |
分析：通过集合的表示法知集合P是函数的定义域，集合Q是函数的值域，化简两个集合；据A+B的定义知求出两集合的并集去掉它们的交集
解答：
解：令x2-3x≥0解得x≥3或x≤0
∴P={x|x≥3或x≤0}
Q={y|y=3x+1}={y|y＞1}
∵A+B={x|x∈A或x∈B且x∉A∩B}，
∴P+Q={x|x≤0或x＞3}
故答案为{x|x≤0或x＞3}
解：令x2-3x≥0解得x≥3或x≤0∴P={x|x≥3或x≤0}
Q={y|y=3x+1}={y|y＞1}
∵A+B={x|x∈A或x∈B且x∉A∩B}，
∴P+Q={x|x≤0或x＞3}
故答案为{x|x≤0或x＞3}
点评：本题考查集合的表示法、求函数的定义域值域、借助数轴求集合的交集并集补集运算．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
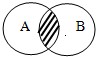1、设A、B为非空集合，定义集合A*B为如图非阴影部分表示的集合，若A={x|y=| 2x-x2 |
| A、（0，2） |
| B、[0，1]∪[2，+∞） |
| C、（1，2] |
| D、[0，1]∪（2，+∞） |
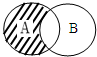设A、B为非空集合，定义运算A*B为如图阴影部分表示的集合，若