Question

（22）

已知数列｛｝中，在直线y=x上，其中n=1，2，3….

(Ⅰ)令

(Ⅱ)求数列

(Ⅲ)设的前n项和。是否存在实数，使得数列为等差数列？若存在，试求出；若不存在，则说明理由。

Answer 1

    (Ⅰ)由已知得  a₁＝，2a_n+1=a_n+n，

    ∵a₂=，a₂-a₁-1=--1＝-，

    又b_n=a_n+1-a_n-1，

    ∴b_n+1=a_n+2-a_n+1-1，

    ∴.

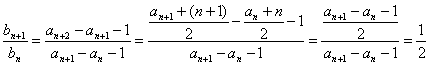    ∴{b_n}是以-为首项，以为公比的等比数列．

    (Ⅱ)由(I)知，b_n＝-×^n-1=-×，

    ∴a_n+1-a_n-1＝-×，

    ∴a₂-a₁-1＝-×，

    a₃-a₂-1=-×，

    ……

    a_n-a_n-1-1=-×，

    将以上各式相加得：

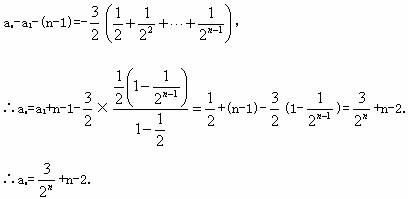
    (Ⅲ)解法一：

    存在λ=2，使数列是等差数列．

    ∵S_n＝a₁+a₂+…+a_n=3+(1+2+…+n)-2n

        =3×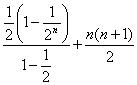-2n

        =3+3．

   

T_n=b₁+b₂+…+b_n=.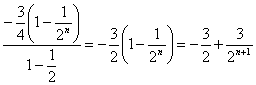

    数列是等差数列的充要条件是=An+B，(A、B是常数)

    即S_n+λT_n=An²+Bn，

    又S_n+λT_n=-+3+λ(-)

             =+3(1-)(1-)

    ∴当且仅当1-＝0，即λ=2时，数列为等差数列.

    解法二：

    存在λ=2，使数列是等差数列.

    由(Ⅰ)、(Ⅱ)知，a_n+2b_n=n-2

    ∴S_n+2T_n=-2n

    ∴

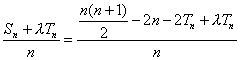
               =T_n

  

  又T_N=b₁+b₂+…+b_n=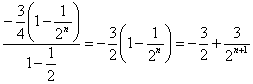

    ∴

    ∴当且仅当λ=2时，数列是等差数列．