题目内容
已知抛物线C:y2=4x,O为坐标原点,动直线l:y=k(x+1)与抛物线C交于A、B两点.
(1)求证:![]() ·
·![]() 为常数;
为常数;
(2)求满足![]() =
=![]() +
+![]() 的点M的轨迹方程.
的点M的轨迹方程.
答案:
解析:
解析:
解析:由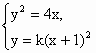 得k2x2+(2k2-4)x+k2=0.
得k2x2+(2k2-4)x+k2=0.
由k≠0.且Δ>0,得-1<1<1,且k≠0.
设A(x1,y1),B(x2,y2),则x1+x2=![]() =-2,x1x2=1.
=-2,x1x2=1.
(1)证明:![]() ·
·![]() =x1x2+y1y2=x1x2+k2(x1+1)(x2+1)
=x1x2+y1y2=x1x2+k2(x1+1)(x2+1)
=(k2+1)x1x2+k2(x1+x2)+k2=k2+1+k2(![]() )+k2=5,
)+k2=5,
∴![]() ·
·![]() =5为常数.
=5为常数.
(2)解:![]() =
=![]() +
+![]() =(x1+x2,y1+y2)=(
=(x1+x2,y1+y2)=(![]() ).
).
设M(x,y),则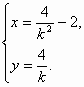 消去k得y2=4x+8.
消去k得y2=4x+8.
又∵x=![]() >2,故M的轨迹方程为y2=4x+8(x>2).
>2,故M的轨迹方程为y2=4x+8(x>2).

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目


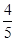 B.
B. C.-
C.-