题目内容
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为
- A.

- B.

- C.
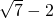
- D.

A
分析:设|BC|=2,|AB|=1,∠ABC=120°,由余弦定理知|AC|= ,由双曲线以A,B为焦点且过点C,知2a=|AC|-|BC|,2c=|AB|.由此能求出双曲线的离心率.
,由双曲线以A,B为焦点且过点C,知2a=|AC|-|BC|,2c=|AB|.由此能求出双曲线的离心率.
解答:设|BC|=2,|AB|=1,∠ABC=120°,由余弦定理知|AC|= ,
,
∵双曲线以A,B为焦点且过点C,
∴ ,2c=|AB|=1,
,2c=|AB|=1,
 .
.
故选A.
点评:本题考查双曲线的离心率,解题时要结合题条件,先求出2a和2c,要注意公式的灵活运用.
分析:设|BC|=2,|AB|=1,∠ABC=120°,由余弦定理知|AC|=
 ,由双曲线以A,B为焦点且过点C,知2a=|AC|-|BC|,2c=|AB|.由此能求出双曲线的离心率.
,由双曲线以A,B为焦点且过点C,知2a=|AC|-|BC|,2c=|AB|.由此能求出双曲线的离心率.解答:设|BC|=2,|AB|=1,∠ABC=120°,由余弦定理知|AC|=
 ,
,∵双曲线以A,B为焦点且过点C,
∴
 ,2c=|AB|=1,
,2c=|AB|=1, .
.故选A.
点评:本题考查双曲线的离心率,解题时要结合题条件,先求出2a和2c,要注意公式的灵活运用.

练习册系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |