题目内容
对于任意实数a、b定义运算“*”,如下a*b=
,则f(x)=log
(3x-2)*log2x的值域为
|
| 1 |
| 2 |
(-∞,0]
(-∞,0]
.分析:根据新定义对于任意实数a、b定义运算“*”,就是取最小值,f(x)=log
(3x-2)*log2x,讨论log
(3x-2)与log2x的大小关系,再根据新定义进行求解;
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:对于任意实数a、b定义运算“*”,如下a*b=
,
其实质就是去最小值,
f(x)=log
(3x-2)*log2x,(x>
)
若log
(3x-2)≥log2x,解得
<x≤1,此时f(x)=log
(3x-2)*log2x=log2x,可得log2
<f(x)≤0,
若log
(3x-2)≤log2x,解得x>1,此时f(x)=log
(3x-2)*log2x=log
(3x-2),可得,log
(3x-2)<0,
综上:f(x)≤0;
故答案为:(-∞,0];
|
其实质就是去最小值,
f(x)=log
| 1 |
| 2 |
| 2 |
| 3 |
若log
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
若log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上:f(x)≤0;
故答案为:(-∞,0];
点评:此题主要考查函数值域的求法,以及新定义的理解,是一道基础题;

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目

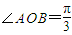 ,求曲线C的方程;
,求曲线C的方程;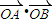 为定值T?指出T的值;
为定值T?指出T的值;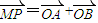 ,当a=-2,m变化时,求点P的轨迹方程;
,当a=-2,m变化时,求点P的轨迹方程; 恒成立?如果存在,求出的M得最小值;如果不存在,说明理由.
恒成立?如果存在,求出的M得最小值;如果不存在,说明理由.