题目内容
((本小题满分12分)
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
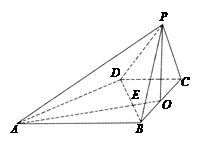
(1)求证:PA⊥BD;
(2)求二面角P—DC—B的大小.
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.

(1)求证:PA⊥BD;
(2)求二面角P—DC—B的大小.
解法一:(1)证明:∵PB=PC,O为BC的中点,
∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD.在梯形ABCD中,
可得Rt△ABO≌Rt△BCD.
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90o,
即AO⊥BD.
∵PA在平面ABCD内的射影为AO,∴PA⊥BD…………………………6分
(2)解:∵DC⊥BC,且平面PBC⊥平面ABCD,
∴DC⊥平面PBC.
∵PC 平面PBC,∴DC⊥PC.
平面PBC,∴DC⊥PC.
∴∠PCB为二面角P—DC—B的平面角.
∵△PCB是等边三角形,
∴∠PCB=60o,即面角P—DC—B的大小为60o……………………12分
解法二:(1)因为△PBC是等边三角形,O是BC的中点,由侧面PBC⊥底面A BCD得PO⊥底面ABCD.以BC中点O为原点,以BC所在直线为x轴,过点与AB平行的直线为y轴,建立如图所示的空间直角坐标系O—xyz.
BCD得PO⊥底面ABCD.以BC中点O为原点,以BC所在直线为x轴,过点与AB平行的直线为y轴,建立如图所示的空间直角坐标系O—xyz.

(1)证明:在直角梯形中,AB="BC=2. "
CD=1,在等边三角形中PBC中,PO= .
.
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0, ).
).
∴ =(-2,-1,
=(-2,-1, 0),
0), =(1,-2,-
=(1,-2,- ).
).
∵ ·
· =(-2)×1+(-1)×(-2)+0×(-
=(-2)×1+(-1)×(-2)+0×(- )=0,
)=0,
∴ ⊥
⊥ ,即PA⊥BD………………………………………………6分
,即PA⊥BD………………………………………………6分
(2)解:取PC的中点N,则N(- ,0,
,0, ).于是
).于是 =(-
=(- ,0,
,0, ).
).
∵C(-1,0,0),∴ =(0,1,0),
=(0,1,0), =(1,0,
=(1,0, ),
),
∴ ·
· =(-
=(- )×1+0×0+
)×1+0×0+ ×
× =0
=0
∴ ⊥平面PDC.显然
⊥平面PDC.显然 =(0,0,
=(0,0, ),且
),且 ⊥平面ABCD.
⊥平面ABCD.
∴ ,
, 所夹角等于所求二面角的平面角.
所夹角等于所求二面角的平面角.
∵ ·
· =(-
=(- )×0+0×0+
)×0+0×0+ ×
× =
= ,
,
| |=
|= ,|
,| |=
|= ,∴cos<
,∴cos< ,
, >=
>= .
.
∴二面角P—DC—B的大小为60o………………………………12分
∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD.在梯形ABCD中,
可得Rt△ABO≌Rt△BCD.
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90o,
即AO⊥BD.
∵PA在平面ABCD内的射影为AO,∴PA⊥BD…………………………6分
(2)解:∵DC⊥BC,且平面PBC⊥平面ABCD,
∴DC⊥平面PBC.
∵PC
 平面PBC,∴DC⊥PC.
平面PBC,∴DC⊥PC.∴∠PCB为二面角P—DC—B的平面角.
∵△PCB是等边三角形,
∴∠PCB=60o,即面角P—DC—B的大小为60o……………………12分
解法二:(1)因为△PBC是等边三角形,O是BC的中点,由侧面PBC⊥底面A
 BCD得PO⊥底面ABCD.以BC中点O为原点,以BC所在直线为x轴,过点与AB平行的直线为y轴,建立如图所示的空间直角坐标系O—xyz.
BCD得PO⊥底面ABCD.以BC中点O为原点,以BC所在直线为x轴,过点与AB平行的直线为y轴,建立如图所示的空间直角坐标系O—xyz.
(1)证明:在直角梯形中,AB="BC=2. "
CD=1,在等边三角形中PBC中,PO=
 .
.∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,
 ).
).∴
 =(-2,-1,
=(-2,-1, 0),
0), =(1,-2,-
=(1,-2,- ).
).∵
 ·
· =(-2)×1+(-1)×(-2)+0×(-
=(-2)×1+(-1)×(-2)+0×(- )=0,
)=0,∴
 ⊥
⊥ ,即PA⊥BD………………………………………………6分
,即PA⊥BD………………………………………………6分(2)解:取PC的中点N,则N(-
 ,0,
,0, ).于是
).于是 =(-
=(- ,0,
,0, ).
).∵C(-1,0,0),∴
 =(0,1,0),
=(0,1,0), =(1,0,
=(1,0, ),
),∴
 ·
· =(-
=(- )×1+0×0+
)×1+0×0+ ×
× =0
=0∴
 ⊥平面PDC.显然
⊥平面PDC.显然 =(0,0,
=(0,0, ),且
),且 ⊥平面ABCD.
⊥平面ABCD.∴
 ,
, 所夹角等于所求二面角的平面角.
所夹角等于所求二面角的平面角.∵
 ·
· =(-
=(- )×0+0×0+
)×0+0×0+ ×
× =
= ,
,|
 |=
|= ,|
,| |=
|= ,∴cos<
,∴cos< ,
, >=
>= .
.∴二面角P—DC—B的大小为60o………………………………12分
略

练习册系列答案
相关题目
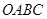 的三条棱
的三条棱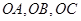 两两垂直,
两两垂直,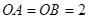 ,
,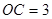 ,
,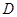 为四面体
为四面体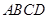 有三个面是直角三角形
有三个面是直角三角形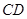 与
与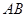 垂直并且相等
垂直并且相等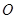 在四面体
在四面体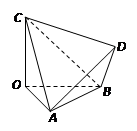
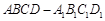 中,棱长都相等;条件乙:直四棱柱
中,棱长都相等;条件乙:直四棱柱 (本小题满分12分)
(本小题满分12分)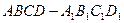 的下底面
的下底面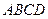 是边长为
是边长为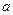 的正方形,
的正方形,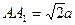 ,且点
,且点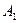 在下底面
在下底面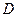 点.
点.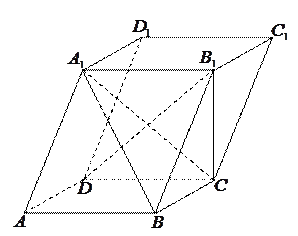
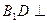 面
面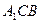 ;
;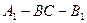 的大小.
的大小. CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD=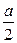 ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .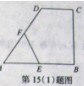
 )
)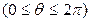 中,曲线
中,曲线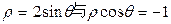 的交点的极坐标为 .
的交点的极坐标为 .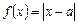 .若不等式
.若不等式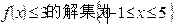 ,则实数
,则实数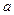 的值为 .
的值为 .