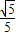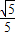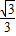题目内容
若2cos2θ+5sinθ•cosθ-3sin2θ=0,θ∈(
,
)则cosθ-sinθ=( )
| π |
| 4 |
| π |
| 2 |
分析:分解因式,结合角的范围可得2cosθ-sinθ=0,结合cos2θ+sin2θ=1,可解得
,相减即可.
|
解答:解:由已知分解因式可得(cosθ+3sinθ)(2cosθ-sinθ)=0,
又θ∈(
,
),故cosθ+3sinθ>0,只能2cosθ-sinθ=0,
结合cos2θ+sin2θ=1,可解得
,
故cosθ-sinθ=-
故选B
又θ∈(
| π |
| 4 |
| π |
| 2 |
结合cos2θ+sin2θ=1,可解得
|
故cosθ-sinθ=-
| ||
| 5 |
故选B
点评:本题考查同角三角函数的基本关系,涉及因式分解的应用,属中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
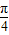 ,
,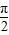 )则cosθ-sinθ=( )
)则cosθ-sinθ=( )