题目内容
已知函数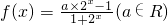 .
.
(I)若a=2,且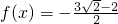 ,求x的值;
,求x的值;
(II)若f(x)为奇函数,求a的值;
(III)当a=5时,函数f(x)的图象是否存在对称中心,若存在,求其对称中心;若不存在,请说明理由.
解:(I)由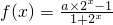 =
=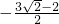 ,得2x=
,得2x= +1,解得x=log2(
+1,解得x=log2( +1).
+1).
(II)由题意知,函数的定义域是R,
∵f(x)为奇函数,∴f(x)=-f(-x),
即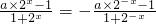 ,即
,即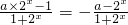 ,
,
解得a=1.
(III)当a=5时,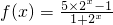 .
.
假设函数f(x)的图象是否存在对称中心,设其坐标为(h,k),
则对任意x∈R,有f(h+x)+f(h-x)=2k恒成立,
即 ,
,
整理得,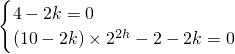 ,
,
解得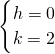 ,
,
当a=5时,函数f(x)的图象存在对称中心,其对称中心为(0,2).
分析:(I)把a=2代入方程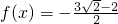 ,再将其转化为指数方程,根据指数函数的性质解指数方程即可.
,再将其转化为指数方程,根据指数函数的性质解指数方程即可.
(II)根据题意求出函数的定义域是R,再由f(x)=-f(-x)列出方程,整理后利用对应项的系数相等,求出a的值.
(III)假设存在对称中心,设其坐标为(h,k),则对任意x∈R,有f(h+x)+f(h-x)=2k恒成立,将函数的解析式代入其中化简求出h,k的值,因而满足条件的实数h,k存在,即存在对称中心.
点评:本题的考点是利用函数奇偶性求值,即利用奇(偶)函数的定义列出方程,化简后由对应项的系数相等求出参数的值,以及对称性问题的处理方法,注意题目中所应用的函数的思想,属于基础题.
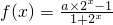 =
=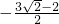 ,得2x=
,得2x= +1,解得x=log2(
+1,解得x=log2( +1).
+1).(II)由题意知,函数的定义域是R,
∵f(x)为奇函数,∴f(x)=-f(-x),
即
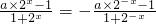 ,即
,即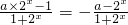 ,
,解得a=1.
(III)当a=5时,
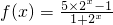 .
.假设函数f(x)的图象是否存在对称中心,设其坐标为(h,k),
则对任意x∈R,有f(h+x)+f(h-x)=2k恒成立,
即
 ,
,整理得,
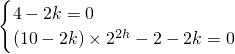 ,
,解得
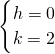 ,
,当a=5时,函数f(x)的图象存在对称中心,其对称中心为(0,2).
分析:(I)把a=2代入方程
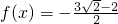 ,再将其转化为指数方程,根据指数函数的性质解指数方程即可.
,再将其转化为指数方程,根据指数函数的性质解指数方程即可.(II)根据题意求出函数的定义域是R,再由f(x)=-f(-x)列出方程,整理后利用对应项的系数相等,求出a的值.
(III)假设存在对称中心,设其坐标为(h,k),则对任意x∈R,有f(h+x)+f(h-x)=2k恒成立,将函数的解析式代入其中化简求出h,k的值,因而满足条件的实数h,k存在,即存在对称中心.
点评:本题的考点是利用函数奇偶性求值,即利用奇(偶)函数的定义列出方程,化简后由对应项的系数相等求出参数的值,以及对称性问题的处理方法,注意题目中所应用的函数的思想,属于基础题.

练习册系列答案
相关题目
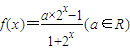 .
.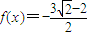 ,求x的值;
,求x的值; .
.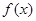 在
在 [1,+∞
[1,+∞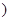 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;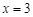 是
是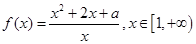 。
。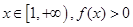 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;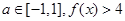 恒成立,求实数x的取值范围。
恒成立,求实数x的取值范围。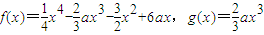 .
.