Question

如图的倒三角形数阵满足：⑴第1行的个数，分别是1，3，5，…，；⑵ 从第二行起，各行

中的每一个数都等于它肩上的两数之和；⑶数阵共有行．问：当时，第32行的第17个数是              ；

 

Answer 1

【答案】

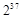
【解析】解：设第k行的第一个数为ak，

则a₁=1，

a₂=4=2a₁+2，

a₃=12=2a₂+2²，

a₄=32=2a₃+2³，

…

由以上归纳，得a_k=2a_k-1+2k-1（k≥2，且k∈N*），

∴a_k 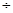2^k =a 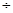_k-1 2^k-1 + ，

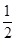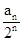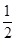∴数列{  }是以 为首项，以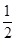为公差的等差数列，

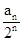∴=1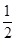+(n-1)×  ，

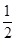∴an=n•2^n-1（n∈N*）．

由数阵的排布规律可知，每行的数（倒数两行另行考虑）都成等差数列，

且公差依次为：2，22，…，2k，…

第n行的首项为an=n•2^n-1（n∈N*），公差为2ⁿ，

∴第32行的首项为a³²=32•2³¹=2³⁶，公差为2³²，

∴第32行的第17个数是2³⁶+16×232=2³⁷．

故答案为：2³⁷．