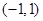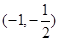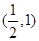题目内容
设函数 ,其中
,其中 ,区间
,区间 .
.
(Ⅰ)求 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 ;
;
(Ⅱ)给定常数 ,当
,当 时,求
时,求 长度的最小值.
长度的最小值.
 ,其中
,其中 ,区间
,区间 .
.(Ⅰ)求
 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 ;
;(Ⅱ)给定常数
 ,当
,当 时,求
时,求 长度的最小值.
长度的最小值.(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
(1)令
解得


 的长度
的长度
(2) 则
则
由 (1)
 ,令
,令 ,得
,得 ,由于
,由于
故 关于
关于 在
在 上单调递增,在
上单调递增,在 上单调递减.,
上单调递减., 必定在
必定在 或
或 处取得
处取得



因此当 时,
时, 在区间
在区间 上取得最小值
上取得最小值 .
.
第(1)题求解一元二次不等式确定区间 的取值范围,根据题意能够求出
的取值范围,根据题意能够求出 的长度,简单题;第(2)题要能理解其实就是求
的长度,简单题;第(2)题要能理解其实就是求 关于
关于 在给定区间内的最小值,通过求导就能确定最小值是当
在给定区间内的最小值,通过求导就能确定最小值是当 取何值,但此题易错点在于需要比较
取何值,但此题易错点在于需要比较 在
在 与
与 处
处 的大小,利用作差或作商都可以解决,出题思路比较新颖,容易迷惑,但只要能够理解题意,基本能够求解出来.
的大小,利用作差或作商都可以解决,出题思路比较新颖,容易迷惑,但只要能够理解题意,基本能够求解出来.
【考点定位】考查二次不等式的求解,以及导数的计算和应用,并考查分类讨论思想和综合运用数学知识解决问题的能力.

解得



 的长度
的长度
(2)
 则
则
由 (1)

 ,令
,令 ,得
,得 ,由于
,由于
故
 关于
关于 在
在 上单调递增,在
上单调递增,在 上单调递减.,
上单调递减., 必定在
必定在 或
或 处取得
处取得


因此当
 时,
时, 在区间
在区间 上取得最小值
上取得最小值 .
.第(1)题求解一元二次不等式确定区间
 的取值范围,根据题意能够求出
的取值范围,根据题意能够求出 的长度,简单题;第(2)题要能理解其实就是求
的长度,简单题;第(2)题要能理解其实就是求 关于
关于 在给定区间内的最小值,通过求导就能确定最小值是当
在给定区间内的最小值,通过求导就能确定最小值是当 取何值,但此题易错点在于需要比较
取何值,但此题易错点在于需要比较 在
在 与
与 处
处 的大小,利用作差或作商都可以解决,出题思路比较新颖,容易迷惑,但只要能够理解题意,基本能够求解出来.
的大小,利用作差或作商都可以解决,出题思路比较新颖,容易迷惑,但只要能够理解题意,基本能够求解出来.【考点定位】考查二次不等式的求解,以及导数的计算和应用,并考查分类讨论思想和综合运用数学知识解决问题的能力.

练习册系列答案
相关题目
 ,则使方程
,则使方程 有解的实数
有解的实数 的取值范围是( )
的取值范围是( )



 的定义域为( )
的定义域为( )



 的定义域是_ ____.
的定义域是_ ____.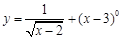 的定义域为
的定义域为  的定义域为( )
的定义域为( )

 时,求
时,求 的值域
的值域 的不等式:
的不等式:
 ,若
,若 ,则( )
,则( ) >
> 
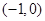 ,则函数
,则函数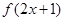 的定义域( )
的定义域( )