题目内容
已知圆O的半径是2,PA,PB为该圆的两条切线,A,B为两个切点,那么
•
的最小值是( )
| PA |
| PB |
A.-24+8
| B.24-8
| C.-12+8
| D.-12-8
|
设PA与PO的夹角为a,则|PA|=|PB|=
,
y=
•
=|
||
|cos2α=
cos2α
=4
cos2α=4
cos2α,
记cos2a=t,则1-t>0,
故y=
=
=4(1-t)+
-12≥2
-12
=8
-12
故选C
| 2 |
| tanα |
y=
| PA |
| PB |
| PA |
| PB |
| 4 |
| tan2α |
=4
| cos2α |
| sin2α |
| 1+cos2α |
| 1-cos2α |
记cos2a=t,则1-t>0,
故y=
| 4t(1+t) |
| 1-t |
| 4(1-t)2-12(1-t)+8 |
| 1-t |
=4(1-t)+
| 8 |
| 1-t |
4(1-t)
|
=8
| 2 |
故选C

练习册系列答案
相关题目
 的最小值是
的最小值是

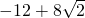

 的最小值是( )
的最小值是( )



 的最小值是( )
的最小值是( )


