题目内容
已知椭圆的焦点坐标为F1(-5,0),F2(5,0),离心率e=
,P为椭圆上一点.
(1)求椭圆的标准方程;
(2)若PF1⊥PF2,求S△PF1F2.
| ||
| 3 |
(1)求椭圆的标准方程;
(2)若PF1⊥PF2,求S△PF1F2.
分析:(1)设出椭圆的方程,利用椭圆的定义得到2a,再利用椭圆的离心率公式列出关于a,c的方程,求出c,利用椭圆中的三个参数的关系求出b,写出椭圆的方程.
(2)利用直角三角形的勾股定理及椭圆的定义得到关于|PF1|,|PF2|的方程,求出|PF1|•|PF2|的值,利用直角三角形的面积公式求出△PF1F2的面积.
(2)利用直角三角形的勾股定理及椭圆的定义得到关于|PF1|,|PF2|的方程,求出|PF1|•|PF2|的值,利用直角三角形的面积公式求出△PF1F2的面积.
解答:解:(1)由题知:c=5,e=
=
,得a=3
,所以b2=a2-c2=20
所以椭圆的标准方程为:
+
=1------------(5分)
(2)由|PF1|+|PF2|=2a=6
,|PF1|2+|PF2|2=|F1F2|2=4c2,可得:
|PF1|•|PF2|=40,所以,S△PF1F2.=
|PF1|•|PF2|=20------------(10分)
| c |
| a |
| ||
| 3 |
| 5 |
所以椭圆的标准方程为:
| x 2 |
| 45 |
| y2 |
| 20 |
(2)由|PF1|+|PF2|=2a=6
| 5 |
|PF1|•|PF2|=40,所以,S△PF1F2.=
| 1 |
| 2 |
点评:求圆锥曲线的方程,一般利用待定系数法,主要考查椭圆的标准方程,以及椭圆的简单性质的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 ,
, ,且短轴一顶点B满足
,且短轴一顶点B满足 ,
, 的直线l与椭圆交于不同的两点M、N,则△
的直线l与椭圆交于不同的两点M、N,则△ MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由。
MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由。 的焦点坐标为
的焦点坐标为 ,长轴等于焦距的2倍.
,长轴等于焦距的2倍. 的边
的边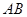 在
在 轴上,点
轴上,点 、
、 落在椭圆
落在椭圆