题目内容
(本小题满分12分)
设函数 ,曲线
,曲线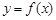 在点(2,
在点(2,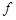 (2))处的切线方程为
(2))处的切线方程为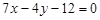
(Ⅰ)求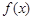 的解析式;
的解析式;
(Ⅱ)若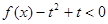 对一切
对一切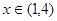 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)证明:曲线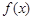 上任一点处的切线与直线
上任一点处的切线与直线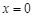 和直线
和直线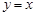 所围成的三角形面积为一值,并求此定值。
所围成的三角形面积为一值,并求此定值。
设函数
 ,曲线
,曲线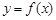 在点(2,
在点(2,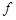 (2))处的切线方程为
(2))处的切线方程为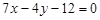
(Ⅰ)求
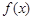 的解析式;
的解析式;(Ⅱ)若
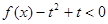 对一切
对一切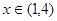 恒成立,求
恒成立,求 的取值范围;
的取值范围;(Ⅲ)证明:曲线
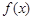 上任一点处的切线与直线
上任一点处的切线与直线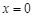 和直线
和直线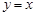 所围成的三角形面积为一值,并求此定值。
所围成的三角形面积为一值,并求此定值。(Ⅰ)
(Ⅱ) 或
或
(Ⅲ)

(Ⅱ)
 或
或
(Ⅲ)

(I)根据点2处的导数值为 和点
和点 .即可建立关于a,b 的方程求出a,b的值,进而确定f(x)的解析式。
.即可建立关于a,b 的方程求出a,b的值,进而确定f(x)的解析式。
(II)不等式恒成立问题转化为 ,然后利用导数求出f(x)的最大值,进而再解关于t的不等式即可。
,然后利用导数求出f(x)的最大值,进而再解关于t的不等式即可。
(III)设任一点(x0,y0),然后利用导数求出其斜率,进而求出其切线方程,然后把面积表示出来,即可确定面积为定值。
 和点
和点 .即可建立关于a,b 的方程求出a,b的值,进而确定f(x)的解析式。
.即可建立关于a,b 的方程求出a,b的值,进而确定f(x)的解析式。(II)不等式恒成立问题转化为
 ,然后利用导数求出f(x)的最大值,进而再解关于t的不等式即可。
,然后利用导数求出f(x)的最大值,进而再解关于t的不等式即可。(III)设任一点(x0,y0),然后利用导数求出其斜率,进而求出其切线方程,然后把面积表示出来,即可确定面积为定值。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目




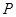 (元)与时间
(元)与时间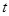 (天)所组成的有序数对
(天)所组成的有序数对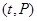 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量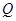 (万股)与时间
(万股)与时间
 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出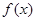 对任意实数
对任意实数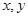 满足:
满足: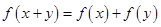 ,且
,且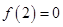 ,则下列结论正确的是_____________.
,则下列结论正确的是_____________.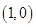 对称;④
对称;④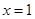 对称.
对称.  的图像先向右平移
的图像先向右平移 个单位,再向下平移两个单位,得到函数
个单位,再向下平移两个单位,得到函数 的图像.
的图像. 的表达式,并求出函数
的表达式,并求出函数 上的单调性和最大值;
上的单调性和最大值; ,
, ,问在
,问在 的图像上是否存在一点
的图像上是否存在一点 ,使得AP⊥BP
,使得AP⊥BP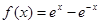 ,
,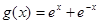
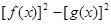 的值;
的值;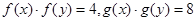 ,求
,求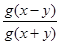 的值。
的值。 的递推关系式是 .
的递推关系式是 . 是定义在R上的可导函数,且对任意的
是定义在R上的可导函数,且对任意的 满足
满足 ,则对任意实数
,则对任意实数 ,下面结论正确的是 ( )
,下面结论正确的是 ( )



 ,若
,若 ,则
,则 ______.
______. ______.
______.