Question

【题目】已知函数（，为自然对数的底数）.

（1）若曲线在点处的切线与直线垂直，求的单调区间；

（2）若函数有两个极值点，求实数的取值范围；

（3）证明：当时，.

Answer 1

【答案】(1)在上单调递增，无单调减区间；(2)；(3)证明见详解.

【解析】

（1）由题意可得切线斜率，也即，据此求得参数，再求的单调区间即可.

（2）若满足题意，只需有两个实数根，分离常数，整理可得只需直线与函数有两个交点即可，数形结合即可求得.

（3）根据（1）中所求，，构造函数，利用导数求其最小值，即可证明.

（1），故可得

由题可得，代值可得，解得.

故，则，

令，解得，

故在区间上单调递减，在区间上单调递增，

故，

即可得在上单调递增，无单调减区间.

（2）函数有两个极值点，等价于有两个不同的实数根.

也即有两个实数根，

即可理解为直线与函数的图像有两个交点.

又，令，解得，

故在区间上单调递增，在区间上单调递减.

故，

又当时，，且趋于正无穷时，趋于0，

当趋于负无穷时，趋于负无穷，

故在同一直角坐标系中绘图如下：

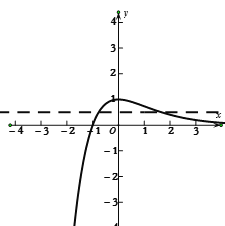
数形结合可知，要满足题意，只需即可.

故的取值范围为.

（3）由（1）可知，当时，，又，

故可得，

要证不等式成立，

只需证当时，即可.

也就是证当时，即可.

又，

因为当时，，故可得，

即可得在上单调递增，

故.

即证当时，，

故当时，成立，即证.