题目内容
以椭圆短轴为直径的圆经过此椭圆的焦点,则椭圆的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由题意可得:b=c,所以a=
=
,进而求出椭圆的离心率.
| b2+c2 |
| 2c |
解答:解:由题意可得:以椭圆短轴为直径的圆经过此椭圆的焦点,
所以b=c,
所以a=
=
,
所以离心率e=
=
.
故选B.
所以b=c,
所以a=
| b2+c2 |
| 2c |
所以离心率e=
| c |
| a |
| ||
| 2 |
故选B.
点评:本题主要考查了椭圆的简单性质.特别是椭圆定义的应用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知椭圆的一个焦点为F,若椭圆上存在点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,点F为椭圆
如图,点F为椭圆 :
: 的左焦点
的左焦点 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于线段
相切于线段 .
. 及椭圆
及椭圆 :
: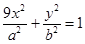 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 两点,设线段
两点,设线段 的中点为
的中点为 ,连结
,连结 ,试问当
,试问当 的直线交椭圆
的直线交椭圆 :
: 于
于 、
、 两点,其中
两点,其中 轴的垂线,垂足为
轴的垂线,垂足为 ,连结
,连结 并延长交椭圆
并延长交椭圆 ,求证:
,求证: