题目内容
已知椭圆 :
: 的左焦点
的左焦点 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于线段
相切于线段 的中点
的中点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知两点 及椭圆
及椭圆 :
: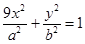 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,设线段
两点,设线段 的中点为
的中点为 ,连结
,连结 ,试问当
,试问当 为何值时,直线
为何值时,直线 过椭圆
过椭圆 的顶点?
的顶点?
(Ⅲ) 过坐标原点 的直线交椭圆
的直线交椭圆 :
: 于
于 、
、 两点,其中
两点,其中 在第一象限,过
在第一象限,过 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连结
,连结 并延长交椭圆
并延长交椭圆 于
于 ,求证:
,求证:
【答案】
(Ⅰ)连接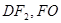
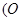 为坐标原点,
为坐标原点,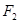 为右焦点),由题意知:椭圆的右焦点为
为右焦点),由题意知:椭圆的右焦点为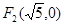 因为
因为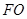 是
是 的中位线,且
的中位线,且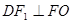 ,所以
,所以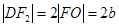
所以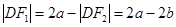 ,故
,故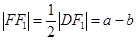 …………2分
…………2分
在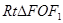 中,
中,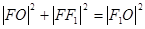
即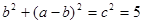 ,又
,又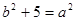 ,解得
,解得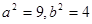
所求椭圆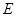 的方程为
的方程为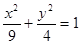 .………………………4分
.………………………4分
(Ⅱ) 由(Ⅰ)得椭圆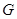 :
: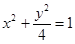
设直线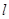 的方程为
的方程为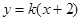 并代入
并代入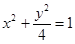
整理得: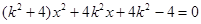
由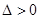 得:
得: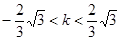 ……………………5分
……………………5分
设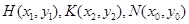
则由中点坐标公式得: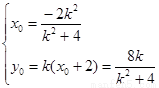 …………………6分
…………………6分
①当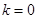 时,有
时,有 ,直线
,直线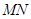 显然过椭圆
显然过椭圆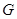 的两个顶点
的两个顶点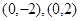 ;………7分
;………7分
②当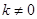 时,则
时,则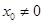 ,直线
,直线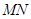 的方程为
的方程为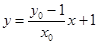
此时直线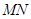 显然不能过椭圆
显然不能过椭圆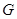 的两个顶点
的两个顶点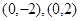 ;
;
若直线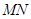 过椭圆
过椭圆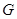 的顶点
的顶点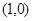 ,则
,则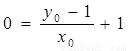 即
即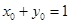
所以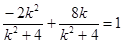 ,解得:
,解得: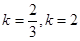 (舍去)………………………8分
(舍去)………………………8分
若直线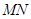 过椭圆
过椭圆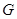 的顶点
的顶点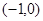 ,则
,则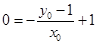 即
即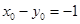
所以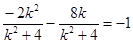 ,解得:
,解得: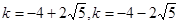 (舍去) ……………9分
(舍去) ……………9分
综上,当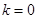 或
或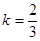 或
或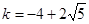 时, 直线
时, 直线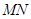 过椭圆
过椭圆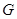 的顶点…………10分
的顶点…………10分
(Ⅲ)法一:由(Ⅰ)得椭圆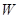 的方程为
的方程为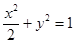 ……………………………11分
……………………………11分
根据题意可设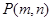 ,则
,则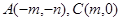
则直线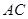 的方程为
的方程为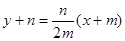 …①
…①
过点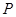 且与
且与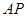 垂直的直线方程为
垂直的直线方程为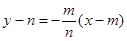 …②
…②
①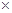 ②并整理得:
②并整理得: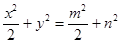
又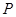 在椭圆
在椭圆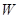 上,所以
上,所以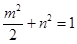 所以
所以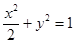
即①、②两直线的交点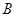 在椭圆
在椭圆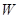 上,所以
上,所以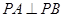 .…………14分
.…………14分
法二:由(Ⅰ)得椭圆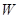 的方程为
的方程为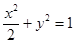
根据题意可设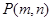 ,则
,则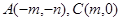 ,
,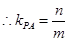 ,
,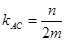
所以直线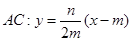
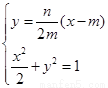 ,化简得
,化简得
所以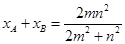
因为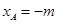 ,所以
,所以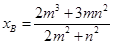 ,则
,则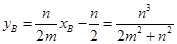 ……………12分
……………12分
所以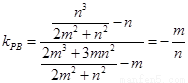 ,则
,则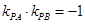 ,即
,即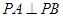
【解析】略

练习册系列答案
相关题目


 :
: 的左焦点为
的左焦点为 ,右焦点为
,右焦点为 .
.
 过点
过点 垂直
垂直 的垂直平分线交
的垂直平分线交 的方程;
的方程; 为坐标原点,取曲线
为坐标原点,取曲线 ,以
,以 为直径作圆与
为直径作圆与 ,求该圆的面积最小时点
,求该圆的面积最小时点 的左焦点为
的左焦点为 (-1,0),离心率为
(-1,0),离心率为 ,过点
,过点 与椭圆C交于
与椭圆C交于 两点.
两点. 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围.