Question

【题目】函数满足，.

（1）若，，求实数的取值范围；

（2）若有三个零点，求实数的取值范围.

Answer 1

【答案】（1）;（2）.

【解析】

（1）由得，求导，构造新函数，讨论确定导函数的符号进而确定函数的最值

（2）利用（1）的讨论判断函数的单调性确定零点个数进而求得的取值范围

（1）∵，∴，∴.

，令，

时，，则，在上单调递增，

∴，，则不合题意；

时，，则，在上单调递减，时，，时，，∴，符合题意；

时，令，设根为、，则，，

不妨设，则有，当时，，则，

在上单调递增，，，则，不合题意.

综上所述，.

（2）时，由（1）在上单调递增，至多一零点，不合题意；

时，由（1）在上单调递减，至多一零点，不合题意；

时，由（1）在上递减，上递增，上递减，此时至多三零点，在上递增，，

令，则，当时，，

令，则，，

当时，；当，，

∴在上单调递减，上单调递增，

∴，∴在上单调递增，

∴，∴，∴，

又，∴，

当时，，∴当时，，

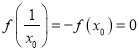∴，，又，，∴存在三个零点，

综上所述，