题目内容

如图，在坐标平面内作两条与实轴平行的直线l1：y=3，l2：y=-1，
它们分别与双曲线
x2
25
-
y2
16
=1的左右两支交于点A1，B1；A2，B2；
F是双曲线的右焦点，则（A1F+A2F）-（B1F+B2F）=
20
20
．
分析：设双曲线的作焦点为F′．由双曲线的对称性可得|F′A1|=|FB1|，|F′A2|=|B2F|．再利用双曲线的定义即可得出．
解答：解：如图所示，设双曲线的作焦点为F′．
由双曲线的对称性可得|F′A1|=|FB1|，|F′A2|=|B2F|．
∴（|A1F|+|A2F|）-（|B1F|+|B2F|）
=(|A1F|-|A1F′|)+(|A2F|-|A2F′|)
=2a+2a=4×5=20．
故答案为20．
点评：熟练掌握双曲线的定义和性质是解题的关键．
练习册系列答案
相关题目
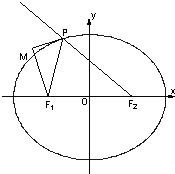精英家教网已知如图，椭圆方程为
x2
16
+
y2
b2
=1（4＞b＞0）．P为椭圆上的动点，
F1、F2为椭圆的两焦点，当点P不在x轴上时，过F1作∠F1PF2的外角
平分线的垂线F1M，垂足为M，当点P在x轴上时，定义M与P重合．
（1）求M点的轨迹T的方程；
（2）已知O（0，0）、E（2，1），试探究是否存在这样的点Q：Q是轨迹T内部的整点（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积S△OEQ=2？若存在，求出点Q的坐标，若不存在，说明理由．
如图展示了一个由区间（0，1）到实数集R的映射过程：区间（0，1）中的实数m对应数轴上的点M，如图1；将线段AB围成一个圆，使两端点A，B恰好重合，如图2；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），如图3．图3中直线AM与x轴交于点N（n，0），则m的像就是n，记作f（m）=n．则在下列说法中正确命题的个数为（　　）
①f（
1
4
）=1；②f（x）为奇函数；③f（x）在其定义域内单调递增；④f（x）的图象关于点（
1
2
，0）对称．
（2012•大丰市一模）如图所示，在直角坐标平面内，反比例函数的图象经过A（1，4），B（a，b），其中a＞1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连接AD、DC、CB．
（1）若△ABD的面积为4，求点B的坐标；
（2）求证：DC∥AB；
（3）四边形ABCD能否为菱形？如果能，请求出四边形ABCD为菱形时，直线AB的函数解析式；如果不能，请说明理由．
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．（几何证明选讲）
如图，已知两圆交于A、B两点，过点A、B的直线分别与两圆交于P、Q和M、N．求证：PM∥QN．
B．（矩阵与变换）
已知矩阵A的逆矩阵A-1=
10
02
，求矩阵A．
C．（极坐标与参数方程）
在平面直角坐标系xOy中，过椭圆
x2
12
+
y2
4
=1在第一象限处的一点P（x，y）分别作x轴、y轴的两条垂线，垂足分别为M、N，求矩形PMON周长最大值时点P的坐标．
D．（不等式选讲）
已知关于x的不等式|x-a|+1-x＞0的解集为R，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网