题目内容
如图,在正方体ABCD—A1B
解析:取BD的中点为O,连结A1O、C1O.
由A1D=A1B,DO=OB,
得A1O⊥BD.同理C1O⊥BD,
∴∠A1OC1为二面角A1BDC1的平面角.
设正方体的棱长为a,连结A![]() a.
a.
在Rt△A1OB中,
A1O=![]() .
.
同理,C1O=![]() .
.
∴cos∠A1OC1=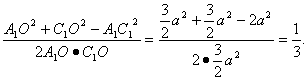
∴∠A1OC1=arccos![]() ,
,
即二面角A1BDC1的大小为arccos![]() .
.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
题目内容
如图,在正方体ABCD—A1B
解析:取BD的中点为O,连结A1O、C1O.
由A1D=A1B,DO=OB,
得A1O⊥BD.同理C1O⊥BD,
∴∠A1OC1为二面角A1BDC1的平面角.
设正方体的棱长为a,连结A![]() a.
a.
在Rt△A1OB中,
A1O=![]() .
.
同理,C1O=![]() .
.
∴cos∠A1OC1=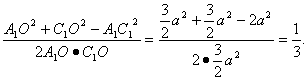
∴∠A1OC1=arccos![]() ,
,
即二面角A1BDC1的大小为arccos![]() .
.

 综合自测系列答案
综合自测系列答案