题目内容
方程2x1+x2+x3+x4+x5+x6+x7+x8+x9+x10=3的非负整数解共有多少个？
解：以特殊的元素x1进行分类：
（1）当x1=1时，x2+x3+x4+x5+x6+x7+x8+x9+x10=1,得其中的一个加数为1，则其余8个加数均为0，所以此时的非负整数解共有9组.
（2）当x1=0时，x2+x3+x4+x5+x6+x7+x8+x9+x10=3,
作变换yi=xi+1,i=2,3,…,10,则y2+y3+y4+y5+y6+y7+y8+y9+y10=12.
于是问题转化为求方程y2+y3+y4+y5+y6+y7+y8+y9+y10=12的正整数解的个数.
由于y2,y3,y4,y5,y6,y7,y8,y9,y10都是正整数，并且它们的和为12，所以可以构造如下模型：设想将12个小球排成一排，它们中间有11个相间空（不含两端），用八个分离器“0”插空，分12个小球成9组，每组分得的小球的个数依次记为y2,y3,y4,y5,y6,y7,y8,y9,y10，每个分法唯一对应着一个正整数解.所以共有插空方法C
=C
=165种.
故方程y2+y3+y4+y5+y6+y7+y8+y9+y10=12的正整数解的个数共有C
=C
=165个.
即当x1=0时，方程2x1+x2+x3+x4+x5+x6+x7+x8+x9+x10=3的非负整数解共有165个.
综合（1）（2）知方程2x1+x2+x3+x4+x5+x6+x7+x8+x9+x10=3的非负整数解共有165+9=174个.
练习册系列答案
超能学典应用题题卡系列答案
相关题目
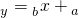至少经过其样本数据点（x1，y1），（x2，y2），…，（xn，yn）中的一个点；
至少经过其样本数据点（x1，y1），（x2，y2），…，（xn，yn）中的一个点；