题目内容
已知向量 =(1,2),
=(1,2), =(2,-2),
=(2,-2),
(1)设 ,求(
,求(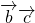 )
) .(2)若
.(2)若 与
与 垂直,求λ的值.(3)求向量
垂直,求λ的值.(3)求向量 在
在 方向上的投影.
方向上的投影.
解:(1)∵ =(1,2),
=(1,2), =(2,-2),
=(2,-2),
∴ =(4,8)+(2,-2)=(6,6).
=(4,8)+(2,-2)=(6,6).
∴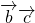 =2×6-2×6=0,
=2×6-2×6=0,
∴(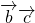 )
) =0
=0 =0.
=0.
(2) =(1,2)+λ(2,-2)=(2λ+1,2-2λ),
=(1,2)+λ(2,-2)=(2λ+1,2-2λ),
由于 与
与 垂直,
垂直,
∴2λ+1+2(2-2λ)=0,
∴λ= .
.
(3)设向量 与
与 的夹角为θ,
的夹角为θ,
向量 在
在 方向上的投影为|a|cosθ.
方向上的投影为|a|cosθ.
∴| |cosθ=
|cosθ= =
= =-
=- =-
=- .
.
分析:(1)利用向量的坐标运算法则求出 的坐标;利用向量的数量积公式求出
的坐标;利用向量的数量积公式求出 .
.
(2)利用向量垂直的充要条件:数量积为0,列出方程求出λ.
(3)利用向量数量积的几何意义得到一个向量在另一个向量方向上的投影公式为两个向量的数量积比上第二个向量的模.
点评:本题考查向量的坐标运算法则、考查向量的数量积公式、考查两个向量垂直的充要条件、考查利用向量的数量积公式求一个向量在另一个向量方向上的投影.
 =(1,2),
=(1,2), =(2,-2),
=(2,-2),∴
 =(4,8)+(2,-2)=(6,6).
=(4,8)+(2,-2)=(6,6).∴
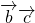 =2×6-2×6=0,
=2×6-2×6=0,∴(
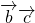 )
) =0
=0 =0.
=0.(2)
 =(1,2)+λ(2,-2)=(2λ+1,2-2λ),
=(1,2)+λ(2,-2)=(2λ+1,2-2λ),由于
 与
与 垂直,
垂直,∴2λ+1+2(2-2λ)=0,
∴λ=
 .
.(3)设向量
 与
与 的夹角为θ,
的夹角为θ,向量
 在
在 方向上的投影为|a|cosθ.
方向上的投影为|a|cosθ.∴|
 |cosθ=
|cosθ= =
= =-
=- =-
=- .
.分析:(1)利用向量的坐标运算法则求出
 的坐标;利用向量的数量积公式求出
的坐标;利用向量的数量积公式求出 .
.(2)利用向量垂直的充要条件:数量积为0,列出方程求出λ.
(3)利用向量数量积的几何意义得到一个向量在另一个向量方向上的投影公式为两个向量的数量积比上第二个向量的模.
点评:本题考查向量的坐标运算法则、考查向量的数量积公式、考查两个向量垂直的充要条件、考查利用向量的数量积公式求一个向量在另一个向量方向上的投影.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知向量
=(1,2),
=(x,2),则向量
+2
与2
-
( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、垂直的必要条件是x=-2 | ||
B、垂直的充要条件是x=
| ||
| C、平行的充分条件是x=-2 | ||
| D、平行的充要条件是x=1 |