题目内容

（2013•延庆县一模）一四面体的三视图如图所示，则该四面体四个面中最大的面积是（　　）
分析：根据三视图，得到四面体的直观图，然后判断四个面中的最大面积即可．
解答：解：将该几何体放入边长为2的正方体中，由三视图可知该四面体为D-BD1C1，由直观图可知，最大的面为BDC1．在正三角形BDC1中，BD=2
2
，
所以面积S=
1
2
×(2
2
)2×
3
2
=2
3
．
故选：D．
点评：本题主要考查三视图的识别和判断，将几何体放入正方体中去研究，是解决本题的关键．
练习册系列答案
相关题目
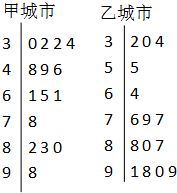（2013•延庆县一模）空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：
PM2.5
日均浓度		 0～35 35～75 75～115 115～150 150～250 ＞250
空气质量级别 一级 二级 三级 四级 五级 六级
空气质量类型 优 良 轻度污染 中度污染 重度污染 严重污染
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测，获得PM2.5日均浓度指数数据如茎叶图所示：
（Ⅰ）根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好？（注：不需说明理由）
（Ⅱ）在15天内任取1天，估计甲、乙两城市空气质量类别均为优或良的概率；
（Ⅲ）在乙城市15个监测数据中任取2个，设X为空气质量类别为优或良的天数，求X的分布列及数学期望．
（2013•延庆县一模）已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的离心率为2，一个焦点与抛物线y2=16x的焦点相同，则双曲线的渐近线方程为（　　）
（2013•延庆县一模）已知函数f（x）=ax3+bx2-2（a≠0）有且仅有两个不同的零点x1，x2，则（　　）
（2013•延庆县一模）已知函数f（x）=
log4x， x＞0
3x， x≤0
，则f[f(
1
16
)]=（　　）
（2013•延庆县一模）如图，四棱锥P-ABCD的底面ABCD为菱形，∠ABC=60°，PA⊥底面ABCD，PA=AB=2，E为PA的中点．
（Ⅰ）求证：PC∥平面EBD；
（Ⅱ）求三棱锥C-PAD的体积VC-PAD；
（Ⅲ）在侧棱PC上是否存在一点M，满足PC⊥平面MBD，若存在，求PM的长；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网