题目内容
(12分)已知函数f(x)＝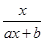
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
f(x)＝
，f[f(－4)]＝
.
解析
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
(12分)已知函数f(x)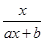＝ (a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
f(x)＝，f[f(－4)]＝.
解析
阅读快车系列答案
，后20天价格为f（t）="45" （31£ t £50, tÎN）,且销售量近似地满足g（t）=" -2t+200" （1£t£50, tÎN）．
的两个函数
的解析式分别为
，
的值域；
的值域．
.
为何实数
总是为增函数；
的单调区间.
的定义域为
，且满足条件：
，②
③当
的值
的x的取值范围。
．
时，求
的单调区间；
时，不等式
恒成立，求实数
的取值范围．
的函数
都有
；
时，
，回答下列问题：
的单调性，并说明理由；
，求
的值.