题目内容
已知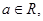 函数
函数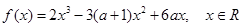
(1)已知任意三次函数的图像为中心对称图形,若本题中的函数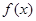 图像以
图像以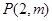 为对称中心,求实数
为对称中心,求实数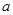 和
和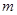 的值
的值
(2)若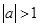 ,求函数
,求函数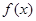 在闭区间
在闭区间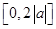 上的最小值
上的最小值
【答案】
(1) ,
, (2)
(2)
【解析】
试题分析:解:(1)由函数 图像以
图像以 为对称中心,则
为对称中心,则 ,代入计算得:
,代入计算得:
 ,故
,故
则
(1)另解:由
则 ,则
,则 ,故
,故
则
(2)由
因为 ,讨论:
,讨论:
1. 若 ,如下表:
,如下表:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
则此时
2. 若 时,如下表:
时,如下表:
|
|
|
1 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
由 ,
,
 当
当 时,
时, ,则
,则
 当
当 时,
时, ,则
,则
综上所述:
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目














 +bx) (a>0且a≠1),则下列叙述正确的是
+bx) (a>0且a≠1),则下列叙述正确的是 ,b=-1,则函数f(x)为R上的增函数
,b=-1,则函数f(x)为R上的增函数