题目内容
8.已知在正方体ABCD-A1B1C1D1中,M、N分别是AA1和BB1的中点,求异面直线CM和D1N所成的角?求异面直线A1M和D1N所成的角?分析 可分别以D1A1,D1C1,D1D三直线为x,y,z轴,建立空间直角坐标系,从而可用空间向量解决本题:可设正方体的边长为2,从而可求出图形上一些点的坐标,从而可以求出向量$\overrightarrow{CM},\overrightarrow{{D}_{1}N},\overrightarrow{{A}_{1}M}$的坐标,这样可求出向量$\overrightarrow{CM}$和$\overrightarrow{{D}_{1}N}$的夹角,$\overrightarrow{{A}_{1}M}$和$\overrightarrow{{D}_{1}N}$的夹角,从而得出对应的异面直线所成角.
解答 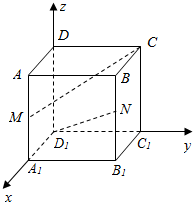 解:如图,分别以边D1A1,D1C1,D1D所在直线为x,y,z轴,建立空间直角坐标系,设正方体的边长为2,则:
解:如图,分别以边D1A1,D1C1,D1D所在直线为x,y,z轴,建立空间直角坐标系,设正方体的边长为2,则:
D1(0,0,0),N(2,2,1),A1(2,0,0),M(2,0,1),C(0,2,2);
∴$\overrightarrow{CM}=(2,-2,-1),\overrightarrow{{D}_{1}N}=(2,2,1)$,$\overrightarrow{{A}_{1}M}=(0,0,1)$;
∴$cos<\overrightarrow{CM},\overrightarrow{{D}_{1}N}>=\frac{-1}{3×3}=-\frac{1}{9}$,cos$<\overrightarrow{{A}_{1}M},\overrightarrow{{D}_{1}N}>$=$\frac{1}{3×1}=\frac{1}{3}$;
∴异面直线CM,D1N所成角为arccos$\frac{1}{9}$,异面直线A1M和D1N所成角为arccos$\frac{1}{3}$.
点评 考查通过建立空间直角坐标系,利用空间向量解决异面直线所成角的问题,能确定空间点的坐标,根据点的坐标可求向量的坐标,向量夹角的余弦公式,并且要弄清异面直线的方向向量的夹角和异面直线所成角的关系.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | 必相交 | B. | 必为异面直线 | C. | 垂直 | D. | 无法确定 |
| A. | 2$\sqrt{3}$ | B. | $\frac{5}{2}$$\sqrt{6}$ | C. | 3$\sqrt{6}$ | D. | $\frac{7\sqrt{7}}{2}$ |
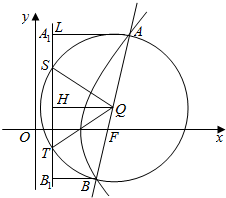 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证: