题目内容
若 ,
, ,lgy成等比数列,则xy的最小值为________.
,lgy成等比数列,则xy的最小值为________.

分析:由lg
 ,
, ,lgy成等比数列,根据等比数列的性质化简后,得到lgx与lgy的积,然后根据基本不等式求出lgx+lgy的最小值,即为lgxy的最小值,进而得到xy的最小值.
,lgy成等比数列,根据等比数列的性质化简后,得到lgx与lgy的积,然后根据基本不等式求出lgx+lgy的最小值,即为lgxy的最小值,进而得到xy的最小值.解答:由lg
 ,
, ,lgy成等比数列,
,lgy成等比数列,得到lg
 •lgy=
•lgy= lgx•lgy=
lgx•lgy= ,即lgx•lgy=
,即lgx•lgy= ,
,所以lgxy=lgx+lgy≥2
 =
= ,当且仅当x=y取等号,
,当且仅当x=y取等号,则xy的最小值为
 .
.故答案为:

点评:此题考查学生灵活运用等比数列的性质化简求值,会利用基本不等式求函数的最小值,掌握对数的运算性质,是一道中档题.

练习册系列答案
相关题目
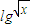 ,
, ,lgy成等比数列,则xy的最小值为 .
,lgy成等比数列,则xy的最小值为 .