题目内容
已知向量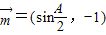 ,
,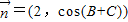 ,A,B,C为锐角△ABC的内角,其对应边为a,b,c.
,A,B,C为锐角△ABC的内角,其对应边为a,b,c.(Ⅰ)当
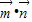 取得最大值时,求角A的大小;
取得最大值时,求角A的大小;(Ⅱ)在(Ⅰ)成立的条件下,当a=
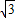 时,求b2+c2的取值范围.
时,求b2+c2的取值范围.
【答案】分析:(I)根据向量数量积的公式,化简得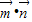 =cosA+2sin
=cosA+2sin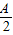 ,结合二倍角的余弦公式化简得
,结合二倍角的余弦公式化简得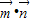 =-(sin
=-(sin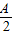 -
- )2+
)2+ ,利用二次函数的性质可得
,利用二次函数的性质可得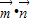 取得最大值时,sin
取得最大值时,sin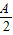 =
= ,结合A为三角形的内角算出A=
,结合A为三角形的内角算出A=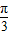 ;
;
(II)由A=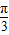 且a=
且a=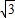 ,利用余弦定理化简得b2+c2-bc=3,根据基本不等式bc≤
,利用余弦定理化简得b2+c2-bc=3,根据基本不等式bc≤ (b2+c2),算出b2+c2≤6.在根据三角形中b+c>a,即可得出b2+c2的取值范围.
(b2+c2),算出b2+c2≤6.在根据三角形中b+c>a,即可得出b2+c2的取值范围.
解答:解:(I)∵向量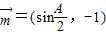 ,
,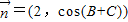 ,
,
∴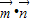 =2sin
=2sin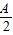 -cos(B+C)
-cos(B+C)
=cosA+2sin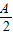 =-2sin2
=-2sin2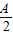 +2sin
+2sin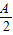 +1=-(sin
+1=-(sin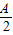 -
- )2+
)2+
因此,当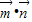 取得最大值时,sin
取得最大值时,sin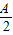 =
= ,
,
结合A为三角形的内角,可得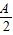 =
=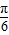 ,得A=
,得A=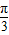 ;
;
(II)在(Ⅰ)成立的条件下,A=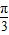
∵a=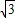 ,∴由余弦定理a2=b2+c2-2bccosA,得b2+c2-bc=3
,∴由余弦定理a2=b2+c2-2bccosA,得b2+c2-bc=3
因此,b2+c2-3=bc≤ (b2+c2),可得b2+c2≤6
(b2+c2),可得b2+c2≤6
当且仅当b=c=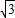 时,等号成立
时,等号成立
又∵△ABC中,b+c>a
∴3<b2+c2≤6,即b2+c2的取值范围(3,6].
点评:本题给出向量含有三角函数式的坐标,求角A的大小并求b2+c2的取值范围,着重考查了向量数量积的坐标公式、余弦定理和基本不等式求最值等知识,属于中档题.
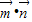 =cosA+2sin
=cosA+2sin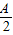 ,结合二倍角的余弦公式化简得
,结合二倍角的余弦公式化简得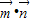 =-(sin
=-(sin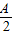 -
- )2+
)2+ ,利用二次函数的性质可得
,利用二次函数的性质可得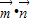 取得最大值时,sin
取得最大值时,sin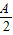 =
= ,结合A为三角形的内角算出A=
,结合A为三角形的内角算出A=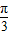 ;
;(II)由A=
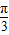 且a=
且a=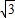 ,利用余弦定理化简得b2+c2-bc=3,根据基本不等式bc≤
,利用余弦定理化简得b2+c2-bc=3,根据基本不等式bc≤ (b2+c2),算出b2+c2≤6.在根据三角形中b+c>a,即可得出b2+c2的取值范围.
(b2+c2),算出b2+c2≤6.在根据三角形中b+c>a,即可得出b2+c2的取值范围.解答:解:(I)∵向量
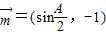 ,
,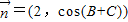 ,
,∴
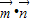 =2sin
=2sin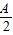 -cos(B+C)
-cos(B+C)=cosA+2sin
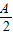 =-2sin2
=-2sin2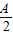 +2sin
+2sin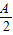 +1=-(sin
+1=-(sin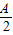 -
- )2+
)2+
因此,当
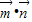 取得最大值时,sin
取得最大值时,sin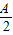 =
= ,
,结合A为三角形的内角,可得
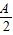 =
=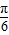 ,得A=
,得A=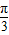 ;
;(II)在(Ⅰ)成立的条件下,A=
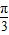
∵a=
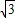 ,∴由余弦定理a2=b2+c2-2bccosA,得b2+c2-bc=3
,∴由余弦定理a2=b2+c2-2bccosA,得b2+c2-bc=3因此,b2+c2-3=bc≤
 (b2+c2),可得b2+c2≤6
(b2+c2),可得b2+c2≤6当且仅当b=c=
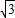 时,等号成立
时,等号成立又∵△ABC中,b+c>a
∴3<b2+c2≤6,即b2+c2的取值范围(3,6].
点评:本题给出向量含有三角函数式的坐标,求角A的大小并求b2+c2的取值范围,着重考查了向量数量积的坐标公式、余弦定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知向量
=(a,b),向量
⊥
且|
|=|
|,则
的坐标为( )
| m |
| m |
| n |
| m |
| n |
| n |
| A、(a,-b) |
| B、(-a,b) |
| C、(b,-a) |
| D、(-b,-a) |
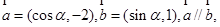 则
则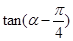 等于(
)
等于(
)  B.
B. C.
C. 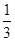 D.
D. 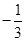
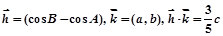 ,其中a、b、c分别是
,其中a、b、c分别是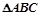 的三内角A、B、C的对边长.
的三内角A、B、C的对边长.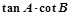 的值;
的值;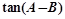 的最大值.
的最大值.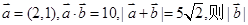 = ( )
= ( )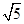 B.
B.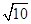 C.5
D.25
C.5
D.25