题目内容
设正四面体ABCD的所有棱长都为1米，有一只蚂蚁从点A开始按以下规则前进：在每一个顶点处等可能的选择通过这个顶点的三条棱之一，并且沿着这条棱爬到尽头，则它爬了4米之后恰好位于顶点A的概率为______．
由题意知本题是一个等可能事件的概率，
假设这个四面体的四个顶点分别为ABCD，蚂蚁从A开始爬．
如果爬到第三次时，蚂蚁在A点，那么第四次就一定不在A点，
∴设蚂蚁第三次在A点的概率为X，那么最后的答案就是
①
设蚂蚁第二次在A点的概率为Y，那么最后的概率就是X=
②
显然蚂蚁第一次爬完之后在A点的概率为0，那么 Y=
③
将③代入②，得X=
=
④
将④代入①得P=
=
故答案为：
假设这个四面体的四个顶点分别为ABCD，蚂蚁从A开始爬．
如果爬到第三次时，蚂蚁在A点，那么第四次就一定不在A点，
∴设蚂蚁第三次在A点的概率为X，那么最后的答案就是
| (1-X) |
| 3 |
设蚂蚁第二次在A点的概率为Y，那么最后的概率就是X=
| 1-Y |
| 3 |
显然蚂蚁第一次爬完之后在A点的概率为0，那么 Y=
| 1-0 |
| 3 |
将③代入②，得X=
1-
| ||
| 3 |
| 2 |
| 9 |
将④代入①得P=
1-
| ||
| 3 |
| 7 |
| 27 |
故答案为：
| 7 |
| 27 |
练习册系列答案
相关题目
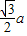；由以上平面图形的特性类比空间图形：设正四面体ABCD的棱长为a，P是正四面体ABCD内的任意一点，且P到四个面ABC、ABD、ACD、BCD的距离分别为d1，d2，d3，d4，则有d1+d2+d3+d4为定值 ．