题目内容
已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(Ⅲ)若![]() ,使
,使![]() (
(![]() )成立,求实数a的取值范围.
)成立,求实数a的取值范围.
解:由已知函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]() .
.
(Ⅰ)函数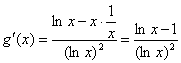
当![]() 且
且![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 的单调减区间是
的单调减区间是![]() ,增区间是
,增区间是![]() . ………………3分
. ………………3分
(Ⅱ)因f(x)在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立.
上恒成立.
所以当![]() 时,
时,![]() .
.
又![]()
![]() ,
,
故当![]() ,即
,即![]() 时,
时,![]() .
.
所以![]() 于是
于是![]() ,故a的最小值为
,故a的最小值为![]() . …………………………6分
. …………………………6分
(Ⅲ)命题“若![]() 使
使![]() 成立”等价于
成立”等价于
“当![]() 时,有
时,有![]() ”.
”.
由(Ⅱ),当![]() 时,
时,![]() ,
,![]()
![]() .
.
问题等价于:“当![]() 时,有
时,有![]() ”. ………………………8分
”. ………………………8分
![]() 当
当![]() 时,由(Ⅱ),
时,由(Ⅱ),![]() 在
在![]() 上为减函数,
上为减函数,
则![]() =
=![]() ,故
,故![]() .
.
![]() 当0<
当0<![]() 时,由于
时,由于![]()
![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 的值域为
的值域为![]() ,即
,即![]() .
.
由![]() 的单调性和值域知,
的单调性和值域知,![]() 唯一
唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时,![]() ,
,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以,![]() =
=![]() ,
,![]() .
.
所以,![]() ,与
,与![]() 矛盾,不合题意.
矛盾,不合题意.
综上,得![]() . …………………………12分[Z
. …………………………12分[Z

 金钥匙试卷系列答案
金钥匙试卷系列答案
 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.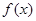 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求