题目内容
给出下列命题:①存在实数x,使得
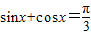 ;
;②函数y=sin2x的图象向右平移
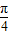 个单位,得到
个单位,得到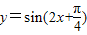 的图象;
的图象;③函数
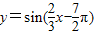 是偶函数;
是偶函数;④已知α,β是锐角三角形ABC的两个内角,则sinα>cosβ.
其中正确的命题的个数为 .
【答案】分析:利用和差角公式,及正弦型函数的值域,可判断①的真假;
根据函数图象的平移规则,结合已知求出平移后函数的解析式,比照后可判断②的真假;
利用诱导公式,将已知函数解析式化为余弦型函数,可判断③的真假;
根据已知临到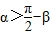 ,进而根据正弦函数的单调性可得④的真假
,进而根据正弦函数的单调性可得④的真假
解答:解:sinx+cosx∈[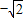 ,
,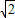 ],
],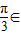 [
[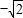 ,
,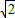 ],故①正确;
],故①正确;
将函数y=sin2x的图象向右平移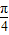 个单位,得到
个单位,得到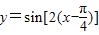 的图象.故②错误;
的图象.故②错误;
函数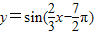 =
=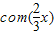 是偶函数,故③正确;
是偶函数,故③正确;
已知α,β是锐角三角形ABC的两个内角,则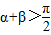 ,则
,则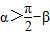 ,sinα>
,sinα>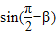 =cosβ,故④正确
=cosβ,故④正确
故答案为:3
点评:本题考查的知识点是三角函数的性质,命题的真假判断与应用,其中熟练掌握三角函数的性质是解答的关键.
根据函数图象的平移规则,结合已知求出平移后函数的解析式,比照后可判断②的真假;
利用诱导公式,将已知函数解析式化为余弦型函数,可判断③的真假;
根据已知临到
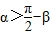 ,进而根据正弦函数的单调性可得④的真假
,进而根据正弦函数的单调性可得④的真假解答:解:sinx+cosx∈[
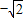 ,
,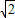 ],
],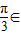 [
[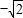 ,
,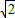 ],故①正确;
],故①正确;将函数y=sin2x的图象向右平移
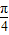 个单位,得到
个单位,得到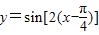 的图象.故②错误;
的图象.故②错误;函数
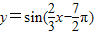 =
=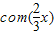 是偶函数,故③正确;
是偶函数,故③正确;已知α,β是锐角三角形ABC的两个内角,则
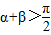 ,则
,则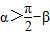 ,sinα>
,sinα>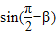 =cosβ,故④正确
=cosβ,故④正确故答案为:3
点评:本题考查的知识点是三角函数的性质,命题的真假判断与应用,其中熟练掌握三角函数的性质是解答的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目