题目内容
在边长为1的正方形ABCD内部随机取一点P,则∠APB>120°的概率是 .
【答案】分析:本题为几何概型,由题意通过圆和三角形的知识画出满足条件的图形,分别找出满足条件的点集对应的图形面积,及图形的总面积,作比值即可.
解答:解: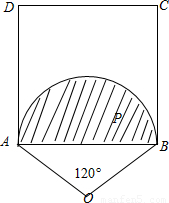
以AB为底边,向正方形外作顶角为120°的等腰三角形,
以等腰三角形的顶点O为圆心,OA为半径作圆,
根据圆周角相关定理,弧AB所对的圆周角为120°.
即当P取圆O与ABCD的公共部分(弓形),∠APB必大于120°
其中AB=1,OA=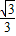 ,O到AB的距离为
,O到AB的距离为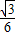 ,
,
故所求的概率为: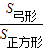 =
=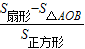
=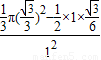 =
=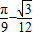 ,
,
故答案为: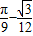
点评:本题考查几何概型,关键是要画出满足条件的图形,结合图形分析,找出满足条件的点集对应的图形面积,及图形的总面积,属中档题.
解答:解:

以AB为底边,向正方形外作顶角为120°的等腰三角形,
以等腰三角形的顶点O为圆心,OA为半径作圆,
根据圆周角相关定理,弧AB所对的圆周角为120°.
即当P取圆O与ABCD的公共部分(弓形),∠APB必大于120°
其中AB=1,OA=
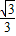 ,O到AB的距离为
,O到AB的距离为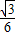 ,
,故所求的概率为:
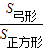 =
=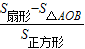
=
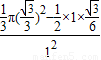 =
=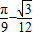 ,
,故答案为:
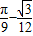
点评:本题考查几何概型,关键是要画出满足条件的图形,结合图形分析,找出满足条件的点集对应的图形面积,及图形的总面积,属中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在边长为1的正方形ABCD中任取一点P,则△ABP的面积大于
的概率是 ( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在边长为1的正方形ABCD内随机取一点P,则点P到点A的距离大于1的概率为( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
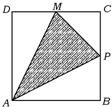
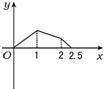
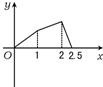
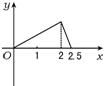
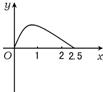
 如右图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是( )
如右图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是( )



 如图,动点P在边长为1的正方形ABCD的边上沿ABCD运动,x表示动点P由A点出发所经过的路程,y表示△APD的面积,则函数y=f(x)的图象的草图是( )
如图,动点P在边长为1的正方形ABCD的边上沿ABCD运动,x表示动点P由A点出发所经过的路程,y表示△APD的面积,则函数y=f(x)的图象的草图是( )