题目内容
6.已知一个平放的正四面体的各棱长均为4,其内有一轻质小球(不计重量),现从正四面体顶端向内注水,球慢慢上浮,当球与正四面体各侧面均相切(与水面也相切)时,若注入的水的体积是正四面体体积的$\frac{7}{8}$,则球的表面积等于.| A. | $\frac{7}{6}$π | B. | $\frac{4}{3}$π | C. | $\frac{2}{3}$π | D. | $\frac{1}{2}$π |
分析 先求出没有水的部分的体积是$\frac{2\sqrt{2}}{3}$,再求出棱长为2,可得小球的半径,即可求出球的表面积.
解答 解:由题意,没有水的部分的体积是正四面体体积的$\frac{1}{8}$,
∵正四面体的各棱长均为4,
∴正四面体体积为$\frac{1}{3}×\frac{\sqrt{3}}{4}×{4}^{2}×\sqrt{16-\frac{16}{3}}$=$\frac{16\sqrt{2}}{3}$,
∴没有水的部分的体积是$\frac{2\sqrt{2}}{3}$,
设其棱长为a,则$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×\frac{\sqrt{6}}{3}a$=$\frac{2\sqrt{2}}{3}$,
∴a=2,
设小球的半径为r,则4×$\frac{1}{3}$×$\frac{\sqrt{3}}{4}×{2}^{2}$r=$\frac{2\sqrt{2}}{3}$,
∴r=$\frac{\sqrt{6}}{6}$,
∴球的表面积S=4$π•\frac{1}{6}$=$\frac{2}{3}π$.
故选:C
点评 本题考查球的表面积,考查体积的计算,考查学生分析解决问题的能力,正确求出半径是关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.使奇函数f(x)=sin(2x+α)在[-$\frac{π}{4}$,0]上为减函数的α的值可以是( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3}{2}$π |
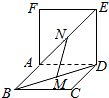 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点,
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、分别是BD和AE的中点, 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作与截面PBC1平行的截面,则截面的面积是2$\sqrt{6}$.