题目内容
 (2011•泉州模拟)某研究性学习小组欲从标点符号使用频率的角度研究《A》名著,现抽查了书中的n页,按每页标点符号的个数把样本分成四组:[30,40),[40,50),[50,60),[60,70),相应的频率分布直方图如图所示,已知样本中[30,40)的频数为1.
(2011•泉州模拟)某研究性学习小组欲从标点符号使用频率的角度研究《A》名著,现抽查了书中的n页,按每页标点符号的个数把样本分成四组:[30,40),[40,50),[50,60),[60,70),相应的频率分布直方图如图所示,已知样本中[30,40)的频数为1.(Ⅰ)求p、n的值;
(Ⅱ)现从这n页中随机抽取3页,用ξ表示标点符号个数在[60,70)的页数,求ξ的分布列和期望.
分析:(I)根据所以频率和为1,即所求小矩形的面积和为1建立等式关系,求出p的值,然后根据等可能事件的概率公式求出n即可;
(II)这10页中标点符号个数在[60,70)有10×0.2=2页,而ξ的可能取值为0,1,2,分别求出相应的概率,根据数学期望公式求出期望即可.
(II)这10页中标点符号个数在[60,70)有10×0.2=2页,而ξ的可能取值为0,1,2,分别求出相应的概率,根据数学期望公式求出期望即可.
解答:解:(Ⅰ)∵p×10+0.03×10+0.04×10+0.02×10=1,
∴p=0.01,
∴标点符号个数在[30,40)的概率为0.1,
∴
=0.1,
∴n=10;
(Ⅱ)这10页中标点符号个数在[60,70)有10×0.2=2页,
又∵ξ的可能取值为0,1,2,P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,
∴ξ的分布列如下:
∴期望Eξ=
.
∴p=0.01,
∴标点符号个数在[30,40)的概率为0.1,
∴
| 1 |
| n |
∴n=10;
(Ⅱ)这10页中标点符号个数在[60,70)有10×0.2=2页,
又∵ξ的可能取值为0,1,2,P(ξ=0)=
| ||
|
| 7 |
| 15 |
| ||||
|
| 7 |
| 15 |
| ||||
|
| 1 |
| 15 |
∴ξ的分布列如下:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 3 |
| 5 |
点评:本题主要考查了离散型随机变量的期望,以及频率分布直方图与等可能事件的概率,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目

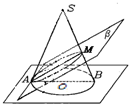 (2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )
(2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )