题目内容
(本小题满分18分,第(1)问6分,第(2)问6分,第(3)问6分)
已知![]() 是虚数,
是虚数,![]() ,且
,且![]() .
.
(1)求![]() 的值及
的值及![]() 的实部的取值范围;
的实部的取值范围;
(2)设![]() ,求证:
,求证:![]() 是纯虚数;
是纯虚数;
(3)求![]() 的最小值.
的最小值.
解 (1)由![]() 是虚数,设
是虚数,设![]() ,
,
则![]() .
.
∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() (b=0舍去),
(b=0舍去),
∴![]() ,∴
,∴![]() ,
,
又![]() 得
得![]() ,即
,即![]() 的实部的取值范围为
的实部的取值范围为![]() .
.
(2)由(1)得![]()
![]() ,
,
∵![]() ,∴
,∴![]() 是纯虚数.
是纯虚数.
(3)由(2)得![]() ,
,
∴![]()
![]() ,当且仅当a=0时取等号.
,当且仅当a=0时取等号.
∴![]() 的最小值为1.
的最小值为1.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成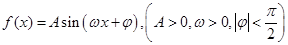 的图象的一部分如下图所示。
的图象的一部分如下图所示。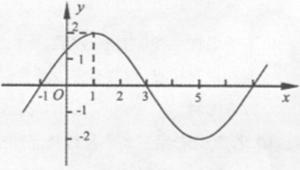
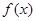 的解析式;
的解析式;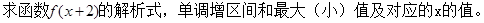
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围;