题目内容
等差数列{an}中,若
=
,则
= .
| a7 |
| a5 |
| 9 |
| 13 |
| S13 |
| S9 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的性质得
=
=
,由等差数列的前n项和公式得
=
×
,代入求值即可.
| a7 |
| a5 |
| 2a7 |
| 2a5 |
| a1+a13 |
| a1+a9 |
| S13 |
| S9 |
| 13 |
| 9 |
| a1+a13 |
| a1+a9 |
解答:
解:由等差数列的性质得,
=
=
=
,
因为S13=
,S9=
所以
=
×
=
×
=1,
故答案为:1.
| a7 |
| a5 |
| 2a7 |
| 2a5 |
| a1+a13 |
| a1+a9 |
| 9 |
| 13 |
因为S13=
| 13(a1+a13) |
| 2 |
| 9(a1+a9) |
| 2 |
所以
| S13 |
| S9 |
| 13 |
| 9 |
| a1+a13 |
| a1+a9 |
| 13 |
| 9 |
| 9 |
| 13 |
故答案为:1.
点评:本题考查等差数列的性质、前n项和公式的灵活应用,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
记事件A发生的概率为P(A),定义f(A)=lg[P(A)+
]为事件A发生的“测度”,现随机抛掷一个骰子,则下列事件中测度最大的一个事件是( )
| 1 |
| P(A) |
| A、向上的点数为2点 |
| B、向上的点数不大于2 |
| C、向上的点数为奇数 |
| D、向上的点数不小于3 |
过点P(2,4)引圆(x-1)2+(y-1)2=1的切线,则切线方程为( )
| A、4x-3y+4=0 |
| B、3x-4y+4=0 |
| C、x-2或4x-3y-4=0 |
| D、x=2或4x-3y+4=0 |
 如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC.
如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC.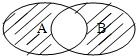 设函数f(x)=lg(1-x2) 集合A={x|y=f(x)},B={y|y=f(x)},则图中阴影部分表示的集合为
设函数f(x)=lg(1-x2) 集合A={x|y=f(x)},B={y|y=f(x)},则图中阴影部分表示的集合为