题目内容
设函数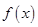 对任意
对任意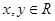 ,都有
,都有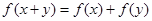 ,当
,当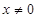 时,
时,
(1)求证: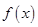 是奇函数;
是奇函数;
(2)试问:在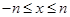 时
时  ,
,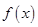 是否有最大值?如果有,求出最大值,如果没有,说明理由.
是否有最大值?如果有,求出最大值,如果没有,说明理由.
(3)解关于x的不等式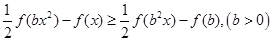
(1)详见解析;(2)函数最大值为 ;(3)①
;(3)① ,则解为
,则解为 ;②
;② ,则解为
,则解为 ;③
;③ ,则无解.
,则无解.
解析试题分析:(1)要证明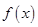 为奇函数,需要证明
为奇函数,需要证明 .如何利用所给条件变出这样一个等式来?
.如何利用所给条件变出这样一个等式来?
为了产生 ,令
,令 ,则
,则 .这时的
.这时的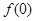 等于0吗?如何求
等于0吗?如何求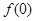 ?再设
?再设 可得
可得 ,从而问题得证.
,从而问题得证.
(2)一个连续函数在闭区间上必最大值的最小值.为了求函数的最值,就需要研究函数的单调性.研究单调性,第一,根据定义,第二利用导数.抽象函数研究单调性只能用定义.任取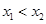 ,则
,则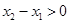 ,根据条件可得:
,根据条件可得: 即
即
所以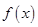 为减函数,那么函数在
为减函数,那么函数在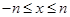 上的最大值为
上的最大值为 .
.
(3)有关抽象函数的不等式,都是利用单调性去掉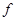 .首先要将不等式化为
.首先要将不等式化为 ,注意必须是左右各一项.在本题中,由题设可得
,注意必须是左右各一项.在本题中,由题设可得 ,
, 在R上为减函数
在R上为减函数 ,即
,即 .下面就解这个不等式.这个不等式中含有参数
.下面就解这个不等式.这个不等式中含有参数 ,故需要分情况讨论.
,故需要分情况讨论.
试题解析:(1)设 可得
可得 ,设
,设 ,则
,则
所以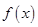 为奇函数.
为奇函数.
(2)任取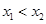 ,则
,则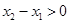 ,又
,又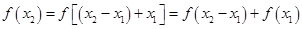
所以
所以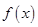 为减函数。
为减函数。
那么函数最大值为 ,
,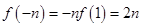 ,
,
所以函数最大值为 .
.
(3)由题设可知
即
可化为
即 ,
, 在R上为减函数
在R上为减函数 ,即
,即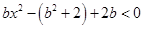 ,
,
① ,则解为
,则解为
② ,则解为
,则解为
③ ,则无解
,则无解
考点:1、抽象函数;2、函数的性质;3、解不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 过点
过点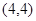 .
. ;
; 的图像向下平移1个单位,再向右平移
的图像向下平移1个单位,再向右平移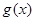 图像,设函数
图像,设函数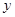 轴对称的函数为
轴对称的函数为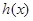 ,试求
,试求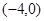 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式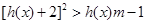 恒成立,求实数
恒成立,求实数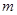 的取值范围.
的取值范围. .
. 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的奇函数
的奇函数 满足
满足 ,且当
,且当 时,
时, .
. 上的解析式;
上的解析式; ,求实数
,求实数 的取值范围.
的取值范围. (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%. 模型制定奖励方案,试用数学语言表述该公司对奖励函数
模型制定奖励方案,试用数学语言表述该公司对奖励函数 模型的基本要求,并分析函数
模型的基本要求,并分析函数 是否符合这个要求,并说明原因;
是否符合这个要求,并说明原因; 作为奖励函数模型,试确定最小的正整数
作为奖励函数模型,试确定最小的正整数 的值.
的值. 是定义域为
是定义域为 的单调减函数,且是奇函数,当
的单调减函数,且是奇函数,当 时,
时,
 的不等式
的不等式
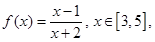
 的单调性,并证明;
的单调性,并证明; 是定义域为R的奇函数.当
是定义域为R的奇函数.当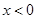 时,
时, ,图像如图所示.
,图像如图所示.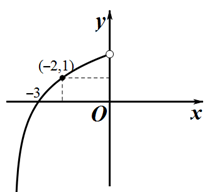
 有两解,写出
有两解,写出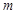 的范围;
的范围; ,写出解集.
,写出解集.
 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 .
. 的值;
的值; ;
; 的值.
的值.