题目内容
已知向量a=(sinθ,cosθ),b=( ,1),其中θ∈(0,
,1),其中θ∈(0, ).
).
(1)若a∥b,求sinθ和cosθ的值;
(2)若f(θ)=(a+b)2,求f(θ)的值域.
(1)sinθ= ,cosθ=
,cosθ= (2)(7,9]
(2)(7,9]
解析解:(1)∵a∥b,
∴sinθ- cosθ=0,
cosθ=0,
求得tanθ= .
.
又∵θ∈(0, ),
),
∴θ= ,sinθ=
,sinθ= ,cosθ=
,cosθ= .
.
(2)f(θ)=(sinθ+ )2+(cosθ+1)2
)2+(cosθ+1)2
=2 sinθ+2cosθ+5
sinθ+2cosθ+5
=4sin(θ+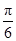 )+5.
)+5.
又∵θ∈(0, ),
),
∴θ+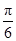 ∈(
∈(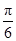 ,
, ),
),
∴ <sin(θ+
<sin(θ+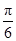 )≤1,
)≤1,
∴7<f(θ)≤9,
即函数f(θ)的值域为(7,9].

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 .
. 的定义域及最小正周期;
的定义域及最小正周期;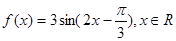
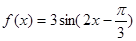 ,
,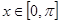 的简图;
的简图;
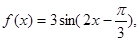
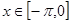 的单调增区间;
的单调增区间;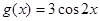 的图象只经过怎样的平移变换就可得到
的图象只经过怎样的平移变换就可得到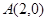 ,
,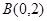 ,
,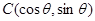 ,
,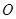 为坐标原点.
为坐标原点.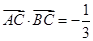 ,求
,求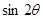 的值;
的值;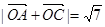 ,且
,且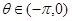 ,求
,求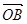 与
与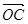 的夹角.
的夹角. 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值. ·sin
·sin cos
cos 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. =-
=- ,求f(x0)的值.
,求f(x0)的值. 的图象经过点
的图象经过点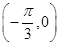 .
.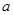 的值;
的值;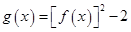 ,求函数
,求函数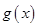 的最小正周期与单调递增区间.
的最小正周期与单调递增区间. .
.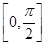 上的最大值和最小值.
上的最大值和最小值.