题目内容
20．（2-x+x2）（1+2x）6的展开式中，x2的系数为109（用数字作答）．分析 先求出（1+2x）6展开式中的常数项、含x的项和含x2的项，再计算（2-x+x2）（1+2x）6的展开式中含x2的系数．
解答 解：∵（2-x+x2）（1+2x）6=（2-x+x2）（1+2${C}_{6}^{1}$•x+4${C}_{6}^{2}$•x2+…），
∴（2-x+x2）（1+2x）6的展开式中，x2的系数为：
2×4${C}_{6}^{2}$-1×2${C}_{6}^{1}$+1×1=109．
故答案为：109．
点评 本题考查了二项式定理的应用问题，是基础题．
练习册系列答案
相关题目
11．为了普及环保知识，共建美丽宜居城市，某市组织了环保知识竞赛，随机抽取了甲、乙两单位中各5名职工的成绩（单位：分）如下表：
（1）根据表中的数据，分别求出甲、乙两个单位这5名职工成绩的平均数和方差，并判断哪个单位的职工对环保知识掌握得更好；（参考公式：样本数据x1，x2，…，xn的方差：${s^2}=\frac{1}{n}[{（{x_1}-\overline x）^2}+{（{x_2}-\overline x）^2}+…+{（{x_n}-\overline x）^2}]$，其中$\overline x$为样本平均数）
（2）用简单随机抽样法从乙单位5名职工中抽取2名，求抽取的2名职工的成绩差的绝对值至少是4的概率．
| 甲单位 | 87 | 88 | 91 | 91 | 93 |
| 乙单位 | 85 | 89 | 91 | 92 | 93 |
（2）用简单随机抽样法从乙单位5名职工中抽取2名，求抽取的2名职工的成绩差的绝对值至少是4的概率．
8．函数y=ln（3x-x3）的单调递增区间是（ ）
| A． | （0，1） | B． | （-1，1） | C． | $（-\sqrt{3}，-1）$ | D． | $（1，\sqrt{3}）$ |
5．如图是一个几何体的三视图，则该几何体的体积是（ ）
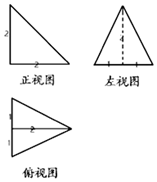
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | $\frac{4}{3}$ |
12．设a，b是两条不同的直线，α，β是两个不同的平面，下列命题正确的是（ ）
| A． | 若a∥b，a∥α，则b∥α | B． | 若α⊥β，a∥α，则a⊥β | C． | 若α⊥β，a⊥β，则a∥α | D． | 若α∥β，m⊥α，则m⊥β |
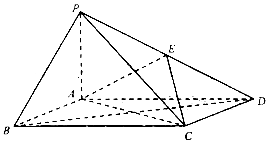如图，在四棱锥P-ABCD中，底面ABCD的平行四边形，∠ADC=60°，$AB=\frac{1}{2}AD$，PA⊥面ABCD，E为PD的中点．