题目内容
已知函数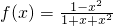 .
.
(1)若(ea+2)x2+eax+ea-2≥0对|x|≤1恒成立,求a的取值范围;
(2)求证:对于正数a、b、μ,恒有f[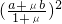 ]-f(
]-f(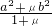 )≥
)≥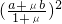 -
-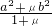 .
.
(1)解:令g(x)=(ea+2)x2+eax+ea-2,
∵g(-1)=ea>0,且对称轴
所以△=e2a-4(e2a-4)≤0
∴3e2a≥16
∴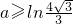
(2)证明:令
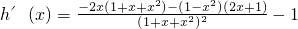 =
=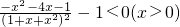
所以函数h(x)在(0,+∞)上是减函数
现证明
只需证明
只需证明a2+μ2b2+2μab≤a2+μb2+μa2+μ2b2
2μab≤μb2+μa2显然成立
∴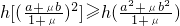
即有f[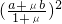 ]-f(
]-f(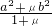 )≥
)≥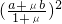 -
-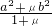
分析:(1)构造函数g(x)=(ea+2)x2+eax+ea-2,确定函数的对称轴,利用判别式,即可求出a的取值范围;
(2)构造函数 ,证明函数h(x)在(0,+∞)上是减函数,将要证明的问题转化为证明
,证明函数h(x)在(0,+∞)上是减函数,将要证明的问题转化为证明 ,即可得结论.
,即可得结论.
点评:本题以函数为载体,考查恒成立问题,考查导数的运用,同时考查了分析法证明不等式,综合性强.
∵g(-1)=ea>0,且对称轴

所以△=e2a-4(e2a-4)≤0
∴3e2a≥16
∴
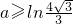
(2)证明:令

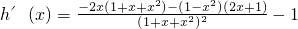 =
=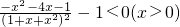
所以函数h(x)在(0,+∞)上是减函数
现证明

只需证明

只需证明a2+μ2b2+2μab≤a2+μb2+μa2+μ2b2
2μab≤μb2+μa2显然成立
∴
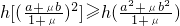
即有f[
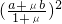 ]-f(
]-f(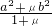 )≥
)≥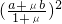 -
-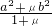
分析:(1)构造函数g(x)=(ea+2)x2+eax+ea-2,确定函数的对称轴,利用判别式,即可求出a的取值范围;
(2)构造函数
 ,证明函数h(x)在(0,+∞)上是减函数,将要证明的问题转化为证明
,证明函数h(x)在(0,+∞)上是减函数,将要证明的问题转化为证明 ,即可得结论.
,即可得结论.点评:本题以函数为载体,考查恒成立问题,考查导数的运用,同时考查了分析法证明不等式,综合性强.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为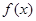 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素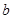 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程