题目内容

椭圆ax²+by²=1与直线y=1-x交于A、B两点，过原点与线段AB中点的直线的斜率为 $数学公式$ ，则 $数学公式$ 的值为________．

$\text{[math]}$
分析：把y=1-x代入椭圆ax²+by²=1得ax²+b（1-x）²=1，由根与系数的关系可以推出线段AB的中点坐标为 $\text{[math]}$ ，再由过原点与线段AB中点的直线的斜率为 $\text{[math]}$ ，能够导出 $\text{[math]}$ 的值．
解答：把y=1-x代入椭圆ax²+by²=1得ax²+b（1-x）²=1，
整理得（a+b）x²-2bx+b-1=0，
设A（x₁，y₁），B（x₂，y₂），则 $\text{[math]}$ ，
∴线段AB的中点坐标为 $\text{[math]}$ ，
∴过原点与线段AB中点的直线的斜率k= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
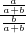答案： $\text{[math]}$ ．
点评：本题考查椭圆的性质及其应用，解题时要注意公式的灵活运用．