题目内容
在△ABC中，M是BC的中点，AM=1，点P在AM上且满足向量
=2
，则向量
（
+
）等于
- A.
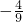
- B.
- C.
- D.
A
分析：由题意M是BC的中点，知AM是BC边上的中线，又由点P在AM上且满足
可得：P是三角形ABC的重心，根据重心的性质，即可求解．
解答：∵M是BC的中点，知AM是BC边上的中线，
又由点P在AM上且满足
∴P是三角形ABC的重心
∴
=
=-
又∵AM=1
∴
=
∴=-
故选A．
点评：本题考查向量的数量积的应用，解题的关键是判断P点是三角形的重心，考查计算能力．
分析：由题意M是BC的中点，知AM是BC边上的中线，又由点P在AM上且满足
可得：P是三角形ABC的重心，根据重心的性质，即可求解．解答：∵M是BC的中点，知AM是BC边上的中线，
又由点P在AM上且满足
∴P是三角形ABC的重心
∴
=
=-又∵AM=1
∴
=∴
=-故选A．
点评：本题考查向量的数量积的应用，解题的关键是判断P点是三角形的重心，考查计算能力．
练习册系列答案
相关题目
＝2
，则
·（
+ 
）等于
）的图象上每点的横坐标和纵坐标都变为原来的
倍，再把图象向右平移
单位，所得图象解析式为y=2sin（2x-
）
等于-4．
上单调递增，函数f（x）在区间
上单调递减．
）的图象上每点的横坐标和纵坐标都变为原来的
倍，再把图象向右平移
单位，所得图象解析式为y=2sin（2x-
）
等于-4．
上单调递增，函数f（x）在区间
上单调递减．