题目内容
求函数f(x)=4x-3•2x+3(-1≤x≤3)的最小值和最大值.
令2x=t,
∵-1≤x≤3,
∴2-1<2x<23,
∴t∈[
,8]
则f(x)=g(t)=t2-3t+3=(t-
)2+
,t∈[
,8]
由二次函数性质f(x)max=g(8)=43,f(x)min=g(
)=
∵-1≤x≤3,
∴2-1<2x<23,
∴t∈[
| 1 |
| 2 |
则f(x)=g(t)=t2-3t+3=(t-
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
由二次函数性质f(x)max=g(8)=43,f(x)min=g(
| 3 |
| 2 |
| 3 |
| 4 |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
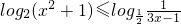 ,求函数f(x)=-4x-2x+1+3的值域.
,求函数f(x)=-4x-2x+1+3的值域.