题目内容
(本小题满分14分)已知椭圆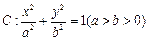 的离心率为
的离心率为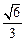 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线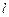 与椭圆
与椭圆 交于
交于 两点,坐标原点
两点,坐标原点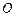 到直线
到直线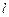 的距离为
的距离为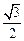 ,求
,求 面积的最大值.
面积的最大值.
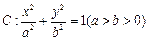 的离心率为
的离心率为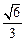 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设直线
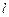 与椭圆
与椭圆 交于
交于 两点,坐标原点
两点,坐标原点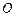 到直线
到直线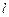 的距离为
的距离为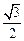 ,求
,求 面积的最大值.
面积的最大值.(Ⅰ)椭圆方程为 (Ⅱ)当
(Ⅱ)当 最大时,
最大时, 面积取最大值
面积取最大值
 (Ⅱ)当
(Ⅱ)当 最大时,
最大时, 面积取最大值
面积取最大值
解:(Ⅰ)设椭圆的半焦距为 ,依题意
,依题意
 ,
, 所求椭圆方程为
所求椭圆方程为 .
.
(Ⅱ)设 ,
, .
.
(1)当 轴时,
轴时, .
.
(2)当 与
与 轴不垂直时,
轴不垂直时,
设直线 的方程为
的方程为 .
.
由已知 ,得
,得 .
.
把 代入椭圆方程,整理得
代入椭圆方程,整理得 ,
,
 ,
, .
.



 .
.
当且仅当 ,即
,即 时等号成立.当
时等号成立.当 时,
时, ,
,
综上所述 .
.
 当
当 最大时,
最大时, 面积取最大值
面积取最大值
 ,依题意
,依题意
 ,
, 所求椭圆方程为
所求椭圆方程为 .
.(Ⅱ)设
 ,
, .
.(1)当
 轴时,
轴时, .
.(2)当
 与
与 轴不垂直时,
轴不垂直时,设直线
 的方程为
的方程为 .
.由已知
 ,得
,得 .
.把
 代入椭圆方程,整理得
代入椭圆方程,整理得 ,
, ,
, .
.


 .
.当且仅当
 ,即
,即 时等号成立.当
时等号成立.当 时,
时, ,
,综上所述
 .
. 当
当 最大时,
最大时, 面积取最大值
面积取最大值

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
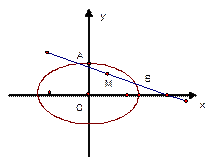
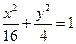 内一点M(1,1)的弦AB
内一点M(1,1)的弦AB 题满分12分)如图所示,已知A、B、C是椭圆
题满分12分)如图所示,已知A、B、C是椭圆 上三点,其中点A的坐标为
上三点,其中点A的坐标为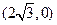 ,BC过椭圆的中心O,且
,BC过椭圆的中心O,且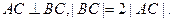
 Q,使得
Q,使得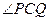 的平分线总垂直于z轴,试判断向量
的平分线总垂直于z轴,试判断向量 是否共线,并给出证明.
是否共线,并给出证明.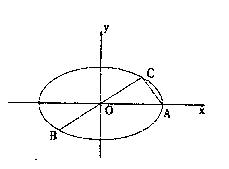
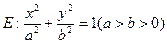 的左、右焦点分别为
的左、右焦点分别为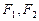 ,点
,点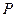 是
是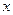 轴上方椭圆
轴上方椭圆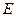 上的一点,且
上的一点,且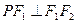 ,
, 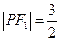 ,
, 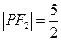 .
.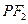 为直径的圆与以椭圆
为直径的圆与以椭圆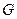 是椭圆
是椭圆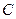 :
: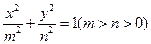 上的任意一点,
上的任意一点,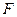 是椭圆
是椭圆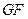 为直径的圆与以椭圆
为直径的圆与以椭圆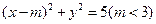 与椭圆E:
与椭圆E: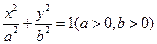 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线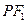 与圆C相切。
与圆C相切。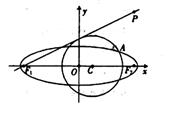
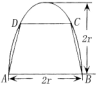
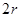 ,短半轴长为
,短半轴长为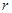 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底 是半椭圆的短轴,上底
是半椭圆的短轴,上底 的端点在椭圆上,记
的端点在椭圆上,记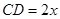 ,梯形面积为
,梯形面积为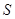 .
.
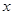 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;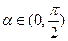 ,方程
,方程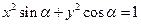 表示焦点在
表示焦点在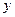 轴上的椭圆,则
轴上的椭圆,则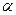 的取值范围是()
的取值范围是()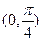
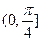
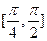
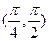
 ,则当
,则当 取得最小值时,椭圆
取得最小值时,椭圆 的离心率是
的离心率是